Inegalitate

Lucrul cu inegalități

Inegalitatea în matematică este atunci când două soluții sau răspunsuri sunt comparate prin mai mare decât sau mai mic decât. Este atunci când cele două sau încă multe soluții care sunt comparate nu sunt de aceeași valoare. Rezolvarea unei inegalități înseamnă găsirea soluțiilor sale. Atunci când înlocuiți un număr cu o variabilă și afirmația este adevărată, atunci este o soluție. Atunci când înlocuiți un număr cu o variabilă și afirmația nu este adevărată, atunci numărul nu este o soluție a afirmației.

Inegalitatea constă în găsirea unei soluții pentru o variabilă dată. Este găsirea unei ordini relative a unui set. Inegalitatea are multe soluții, dar trebuie să găsiți soluțiile reale. Inegalitatea este rezolvarea numerelor reale. Modul corect de citire a inegalităților este de la stânga la dreapta, la fel ca celelalte ecuații, dar singura diferență este că au reguli diferite pentru fiecare ecuație.

De exemplu, x+4>12, unde x este un număr real. Mai întâi, o persoană trebuie să găsească x și trebuie să știe dacă este o soluție. Răspunsul va fi x>8 și este o afirmație adevărată. Această expresie se referă la locația lui x în cadrul setului de numere reale. O dreaptă numerică este o modalitate de a arăta locația în raport cu toate celelalte numere reale.(A se vedea figura Inegalitatea 1)

Inegalitatea 1 Aceasta este soluția pentru ecuația x+4>12

Diferite tipuri de inegalități

Există cinci tipuri diferite de inegalități:

1. Prima este inegalitatea liniară, care este o inegalitate care diferențiază expresiile fie mai mică sau egală cu, mai mică decât sau mai mare decât sau egală cu, mai mare decât. Este una care, dacă înlocuim inegalitatea cu relația egalitate, atunci rezultatul va fi o ecuație liniară.
2. A doua este combinațiile de inegalități care, pentru a satisface inegalitățile, trebuie să aveți un număr în seturile de soluții, astfel încât numerele care satisfac inegalitățile să fie valorile din intersecția celor două seturi de soluții.
3. Cea de-a treia este inegalitățile care implică valori absolute, ceea ce înseamnă că valorile pot fi reformulate ca combinații de inegalități care vor implica valori absolute.
4. Cea de-a patra se numește inegalitate polinomială, ceea ce înseamnă că este continuă, adică graficele lor nu au salturi sau întreruperi.
5. Ultima, dar nu cea din urmă, este inegalitatea rațională, ceea ce înseamnă că este forma unuia dintre polinomii împărțit la un polinom. Cu alte cuvinte, graficele funcțiilor raționale nu au întreruperi și nici nu reprezintă la zerourile numitorului.

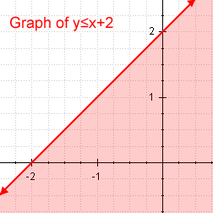
Inegalitate liniară Exemplu de inegalitate liniară


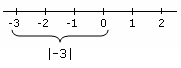
valoare absolută Exemplu care arată valoarea absolută

Patru moduri de rezolvare a inegalităților

Există patru moduri de a rezolva ecuațiile pătratice:

1. Regula numărul unu este că trebuie să adăugați sau să scădeți același număr pe ambele părți.
2. Regula numărul doi este că trebuie să mutați laturile și să schimbați poziționarea semnului inegalității.
3. Regula numărul trei este că trebuie să înmulțești.
4. Regula numărul patru este de a împărți același număr pozitiv sau negativ în ambele părți. Dar, puteți folosi aceste reguli doar în cazul problemelor ușoare de inegalitate.

În plus, este nevoie de doi pași pentru a rezolva o inegalitate. Primul constă în simplificarea folosind reciproca adunării sau a scăderii. Al doilea constă în simplificarea și mai mult prin utilizarea reciprocă a înmulțirii sau a împărțirii. Atunci când înmulțiți sau împărțiți o inegalitate cu un număr negativ, nu uitați să întoarceți simbolul inegalității.

Un exemplu de adunare a inegalităților.


exemplu de multiplicare a inegalității

Exemple de rezolvare a inegalităților

Inegalitatea este o afirmație matematică care explică faptul că cele două valori nu sunt egale și diferite. Ecuația ab înseamnă că a nu este egal cu b. Inegalitatea este identică cu orice ecuație, dar singura diferență este că inegalitatea nu folosește semnul egal, ci simboluri. Inegalitatea b>a reprezintă faptul că b este mai mare decât a. Limitele de viteză,marcajul și altele folosesc inegalitatea pentru a le exprima.

Atunci când se rezolvă o inegalitate, o persoană trebuie să aibă o afirmație adevărată. Atunci când împărțiți sau înmulțiți o inegalitate cu un număr negativ pe ambele părți, afirmația este falsă.Pentru a face afirmația corectă cu un număr negativ, trebuie să inversați simbolul pentru a face afirmația corectă. Atunci când un număr este un număr pozitiv, nu este nevoie să inversați simbolul. Inegalitatea constă în a face o afirmație adevărată.

De exemplu, începeți cu o afirmație adevărată -6y<-12. Când ambele părți sunt împărțite la -6, rezultatul va fi y< 2. În acest enunț, simbolul trebuie inversat pentru a obține un enunț adevărat, y>2 este răspunsul corect. În linia numerelor (vezi figura Inegalitatea 2), un cerc închis și umbrit indică faptul că este inclus în setul de soluții. Un cerc deschis indică faptul că nu este inclus în setul de soluții.

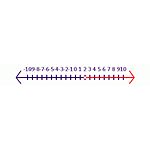
Inegalitatea 2 Soluția pentru ecuația -6y<-12

Pagini conexe

• Egalitate (matematică)
• Ecuația