Regresie liniară | o modalitate de a vedea cum se schimbă ceva atunci când alte lucruri se schimbă folosind matematica

Autor: Leandro Alegsa

28-12-2022

Regresia liniară este o modalitate de a observa modul în care se schimbă ceva atunci când alte lucruri se schimbă folosind matematica. O regresie liniară utilizează o variabilă dependentă și una sau mai multe variabile explicative pentru a crea o linie dreaptă. Această linie dreaptă este cunoscută sub numele de "linie de regresie".

Regresia liniară a fost prima dintre numeroasele modalități de efectuare a analizei de regresie. Acest lucru se datorează faptului că modelele care depind în mod liniar de parametrii lor necunoscuți sunt mai ușor de ajustat decât modelele care sunt legate în mod neliniar de parametrii lor. Un alt avantaj al regresiei liniare este acela că proprietățile statistice ale estimatorilor rezultați sunt mai ușor de determinat.

Regresia liniară are multe utilizări practice. Cele mai multe aplicații se încadrează într-una dintre următoarele două mari categorii:

Regresia liniară poate fi utilizată pentru a ajusta un model predictiv la un set de valori observate (date). Acest lucru este util, dacă obiectivul este predicția, prognoza sau reducerea. După dezvoltarea unui astfel de model, dacă se dă apoi o valoare suplimentară a lui X fără valoarea y care o însoțește, modelul ajustat poate fi utilizat pentru a realiza o valoare prezisă a lui y (scrisă ca y ^ {\displaystyle {\hat {y}}} ${\hat {y}}$ ).
Având în vedere o variabilă y și un număr de variabile X₁ , ..., X_p care pot fi legate de y, analiza de regresie liniară poate fi aplicată pentru a cuantifica intensitatea relației dintre y și X_j , pentru a evalua care X_j nu are nicio relație cu y și pentru a identifica ce subansambluri ale X_j conțin informații redundante despre y.

Modelele de regresie liniară încearcă să facă ca distanța verticală dintre linie și punctele de date (adică reziduurile) să fie cât mai mică posibil. Acest lucru se numește "adaptarea dreptei la date". Adesea, modelele de regresie liniară încearcă să minimizeze suma pătratelor reziduurilor (cele mai mici pătrate), dar există și alte modalități de ajustare. Acestea includ minimizarea "lipsei de potrivire" într-o altă normă (ca în cazul regresiei cu cele mai mici abateri absolute) sau minimizarea unei versiuni penalizate a funcției de pierdere a celor mai mici pătrate, ca în cazul regresiei ridge. Abordarea celor mai mici pătrate poate fi utilizată și pentru a ajusta modele care nu sunt liniare. După cum s-a subliniat mai sus, termenii "cele mai mici pătrate" și "model liniar" sunt strâns legați, dar nu sunt sinonime.

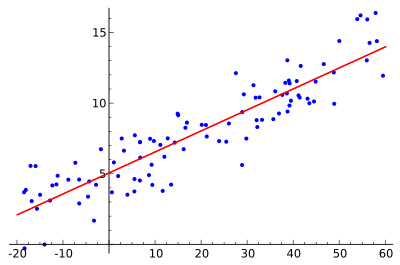
Ideea este de a găsi curba roșie, iar punctele albastre sunt eșantioane reale. În cazul regresiei liniare, toate punctele pot fi conectate folosind o singură linie dreaptă. Acest exemplu utilizează o regresie liniară simplă, în care pătratul distanței dintre linia roșie și fiecare punct de eșantionare este minimizat.

Utilizare

Economie

Regresia liniară este principalul instrument analitic în economie. De exemplu, este utilizată pentru a ghici cheltuielile de consum, cheltuielile pentru investiții fixe, investițiile în stocuri, achizițiile de exporturi ale unei țări, cheltuielile pentru importuri, cererea de a deține active lichide, cererea și oferta de forță de muncă.

Pagini conexe

Ajustarea curbei
Regresie logistică
Cel mai mic pătrat ordinar

Întrebări și răspunsuri

Î: Ce este regresia liniară?

R: Regresia liniară este un mod de a observa cum se schimbă ceva atunci când alte lucruri se schimbă, folosind matematica. Ea utilizează o variabilă dependentă și una sau mai multe variabile explicative pentru a crea o linie dreaptă, cunoscută sub numele de "linie de regresie".

Î: Care sunt avantajele regresiei liniare?

R: Modelele care depind liniar de parametrii lor necunoscuți sunt mai ușor de ajustat decât modelele care sunt legate neliniar de parametrii lor. În plus, proprietățile statistice ale estimatorilor rezultați sunt mai ușor de determinat.

Î: Care sunt câteva utilizări practice ale regresiei liniare?

R: Regresia liniară poate fi utilizată pentru a ajusta un model predictiv la valorile observate (date) pentru a face predicții, prognoze sau reduceri. De asemenea, poate fi utilizată pentru a cuantifica puterea relațiilor dintre variabile și pentru a identifica subseturile de date care conțin informații redundante despre o altă variabilă.

Î: Cum încearcă modelele de regresie liniară să minimizeze erorile?

R: Modelele de regresie liniară încearcă să facă ca distanța verticală dintre linie și punctele de date (reziduurile) să fie cât mai mică posibil. Acest lucru se realizează prin minimizarea fie a sumei pătratelor reziduurilor (cele mai mici pătrate), fie a lipsei de potrivire într-o altă normă (cele mai mici abateri absolute), fie prin minimizarea unei versiuni penalizate a funcției de pierdere a celor mai mici pătrate (regresie ridge).

Î: Este posibil ca modelele de regresie liniară să nu se bazeze pe metoda celor mai mici pătrate?

R: Da, este posibil ca modelele de regresie liniară să nu se bazeze pe metoda celor mai mici pătrate, ci să utilizeze în schimb metode precum minimizarea lipsei de potrivire într-o altă normă (cele mai mici abateri absolute) sau minimizarea unei versiuni penalizate a funcției de pierdere a celor mai mici pătrate (regresie ridge).

Î: Sunt "model liniar" și "cele mai mici pătrate" sinonime?

R: Nu, nu sunt sinonime. Deși sunt strâns legate între ele, "model liniar" se referă în mod specific la utilizarea unei linii drepte, în timp ce "cele mai mici pătrate" se referă în mod specific la încercarea de a minimiza erorile, asigurându-se că există o distanță verticală minimă între linie și punctele de date.