Adaptarea curbei
Ajustarea curbei constă în construirea unei funcții matematice care se potrivește cel mai bine unui set de puncte de date.
Ajustarea curbei poate implica fie interpolare, fie netezire. Utilizarea interpolării necesită o potrivire exactă a datelor. În cazul netezitului, se construiește o funcție "netedă", care se potrivește aproximativ datelor. Un subiect înrudit este analiza de regresie, care se concentrează mai mult pe chestiuni de inferență statistică, cum ar fi cât de multă incertitudine este prezentă într-o curbă care se potrivește la date observate cu erori aleatorii.
Curbele ajustate pot fi utilizate pentru a ajuta la vizualizarea datelor, pentru a ghici valorile unei funcții în cazul în care nu sunt disponibile date și pentru a rezuma relațiile dintre două sau mai multe variabile. Extrapolarea se referă la utilizarea unei curbe ajustate dincolo de intervalul datelor observate. Aceasta este supusă unui anumit grad de incertitudine, deoarece poate reflecta metoda utilizată pentru construirea curbei la fel de mult ca și datele observate.
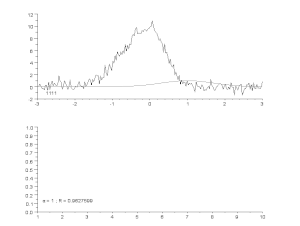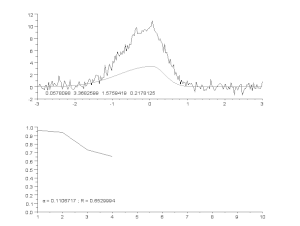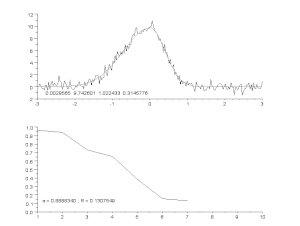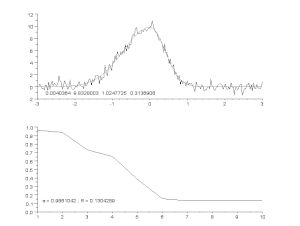
Ajustarea unei curbe zgomotoase cu un model de vârf asimetric, cu un proces iterativ (algoritmul Gauss-Newton cu factor de amortizare variabil α). Sus: date brute și model. Jos: evoluția sumei normalizate a pătratelor pătratelor erorilor.
Întrebări și răspunsuri
Î: Ce este ajustarea curbei?
R: Adaptarea curbelor este procesul de creare a unei funcții matematice care se potrivește cel mai bine unui set de puncte de date.
Î: Care sunt cele două tipuri de ajustare a curbelor?
R: Cele două tipuri de ajustare a curbelor sunt interpolarea și netezirea.
Î: Ce este interpolarea?
R: Interpolarea este un tip de ajustare a curbelor care necesită o potrivire exactă a datelor.
Î: Ce este netezirea?
R: Netezirea este un tip de ajustare a curbelor care construiește o funcție "netedă" care se potrivește aproximativ datelor.
Î: Ce este analiza de regresie?
R: Analiza de regresie este un subiect conex care se concentrează pe chestiuni de inferență statistică, cum ar fi cât de multă incertitudine este prezentă într-o curbă care se potrivește la date observate cu erori aleatorii.
Î: Care sunt unele utilizări ale curbelor ajustate?
R: Curbele ajustate pot fi utilizate pentru a ajuta la vizualizarea datelor, pentru a ghici valorile unei funcții în cazul în care nu sunt disponibile date și pentru a rezuma relațiile dintre două sau mai multe variabile.
Î: Ce este extrapolarea?
R: Extrapolarea este utilizarea unei curbe ajustate dincolo de intervalul de variație al datelor observate. Cu toate acestea, acest lucru este supus unui anumit grad de incertitudine, deoarece poate reflecta metoda utilizată pentru construirea curbei la fel de mult ca și datele observate.
Căuta în