Set | o idee din matematică

Un set este o idee din matematică. Un set are membri (numiți și elemente). Un set este definit de membrii săi, astfel încât orice două seturi cu aceiași membri sunt identice (de exemplu, dacă setul X {\displaystyle {\mathit {X}}} ${\mathit {X}}$ și setul Y {\displaystyle {\mathit {Y}}} ${\mathit {Y}}$ au aceiași membri, atunci X = Y {\displaystyle {\mathit {X}}={\mathit {Y}}} ${\mathit {X}}={\mathit {Y}}$ ).

Un set nu poate avea același membru de mai multe ori. Apartenența este singurul lucru care contează. De exemplu, nu există nicio ordine sau altă diferență între membri. Orice lucru poate fi membru al unui set, inclusiv seturile însele (deși, dacă un set este membru al lui însuși, pot apărea paradoxuri precum paradoxul lui Russell).

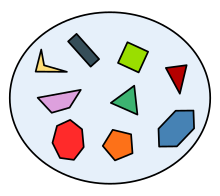
Exemplu de set de poligoane

Georg Cantor, în 1894. Cantor a fost primul matematician care a vorbit despre seturi

Definiția originală a lui Cantor a unui set

Ce se face cu seturile

Imaginați-vă că setul este o geantă.

Element de

Într-o pungă pot fi puse diverse lucruri. Mai târziu, o întrebare bună ar fi dacă un anumit lucru se află în pungă. Matematicienii numesc acest element de. Ceva este un element al unui set, dacă acel lucru poate fi găsit în sacul respectiv. Simbolul folosit pentru acest lucru este ∈ {\displaystyle \in } $\in$ :

a ∈ A {\displaystyle a\in {\mathit {A}}}} $a\in {\mathit {A}}$ ,

ceea ce înseamnă că un {\displaystyle a} se află în sacul A {\displaystyle {\mathit {A}}} ${\mathit {A}}$ sau un {\displaystyle a} este un element din A {\displaystyle {\mathit {A}}} ${\mathit {A}}$ .

Spre deosebire de un sac, un set poate conține cel mult un singur element de un anumit tip. Astfel, în cazul unui set de fructe, nu contează dacă există o singură portocală sau 10 portocale.

Set gol

La fel ca o pungă, un set poate fi și gol. Setul gol este ca o pungă goală: nu are nimic în ea. "Setul gol" se mai numește și set nul și este reprezentat prin simbolul ∅ {\displaystyle \varnothing } $\varnothing$ .

Univers

Dacă luăm în considerare, să zicem, unele seturi de mașini americane, de exemplu un set de toate Ford-urile și un set de toate Dodge-urile, am putea dori, de asemenea, să luăm în considerare întregul set de mașini americane. În acest caz, ansamblul tuturor mașinilor americane ar fi numit univers.

Cu alte cuvinte, un univers este o colecție de toate elementele pe care se dorește să le ia în considerare într-o anumită problemă. Universul se numește de obicei U {\displaystyle U} $U$ .

Compararea seturilor

Se pot compara două seturi. Este ca și cum te-ai uita în două genți diferite. Dacă acestea conțin aceleași lucruri, sunt egale. Nu contează, în ce ordine sunt aceste lucruri.

De exemplu, dacă A = { S t a n f o r d , S t a n l e y } {\displaystyle {\mathit {A}}=\{Stanford,Stanley\}}} ${\mathit {A}}=\{Stanford,Stanley\}$ și B = { S t a n l e y , S t a n f o r d } {\displaystyle {\mathit {B}}=\{Stanley,Stanford\}} ${\mathit {B}}=\{Stanley,Stanford\}$ , seturile sunt aceleași.

Cardinalitatea unui set

Atunci când matematicienii vorbesc despre un set, ei doresc uneori să știe cât de mare este un set (sau care este cardinalitatea setului). Ei fac acest lucru numărând câte elemente se află în set (câte elemente sunt în geantă). Pentru seturile finite, cardinalitatea este un număr simplu. Setul gol are o cardinalitate de 0. Setul { a p l e , o r a n g e } {\displaystyle \{apple,orange\}} $\{apple,orange\}$ are cardinalitatea 2.

Două seturi au aceeași cardinalitate dacă putem împerechea elementele lor - dacă putem uni două elemente, unul din fiecare set. Setul { a p l e , o r a n g e } {\displaystyle \{apple,orange\}} $\{apple,orange\}$ și setul { s u n , m o o o n } {\displaystyle \{sun,moon\}}} $\{sun,moon\}$ au aceeași cardinalitate. De exemplu, am putea asocia mărul cu soarele și portocala cu luna. Ordinea nu contează. Este posibil să se împerecheze toate elementele și niciunul nu este omis. Dar setul { d o g , c a t , b i r d } {\displaystyle \{dog,cat,bird\}} $\{dog,cat,bird\}$ și setul { 5 , 6 } {\displaystyle \{5,6\}} $\{5,6\}$ au cardinalitate diferită. Dacă încercăm să le împerechem, vom omite întotdeauna un animal.

Cardinalitate infinită

Uneori, cardinalitatea nu este un număr. Uneori, un set are o cardinalitate infinită. Ansamblul tuturor numerelor întregi este un ansamblu cu cardinalitate infinită. Unele seturi cu cardinalitate infinită sunt mai mari (au o cardinalitate mai mare) decât altele. De exemplu, există mai multe numere reale decât numere naturale, ceea ce înseamnă că nu putem împerechea setul de numere întregi și setul de numere reale, chiar dacă am lucra la nesfârșit.

Contabilitate

Dacă se pot număra elementele unui ansamblu, acesta se numește ansamblu numărabil. Seturile numărabile includ toate seturile cu un număr finit de membri. Seturile numărabile includ, de asemenea, unele seturi infinite, cum ar fi numerele naturale. Puteți număra numerele naturale cu 1 , 2 , 3 ... {\displaystyle {1,2,3...}}} ${1,2,3...}$ . Numerele naturale sunt supranumite "numerele de numărat", deoarece acestea sunt cele cu care folosim de obicei pentru a număra lucruri.

Un set nenumărabil este un set infinit care nu poate fi numărat. Dacă încercăm să numărăm elementele, vom omite întotdeauna unele. Nu contează ce pas facem. Setul numerelor reale este un set nenumărabil. Există multe alte seturi nenumărabile, chiar și un interval atât de mic precum [ 0 , 1 ] {\displaystyle [0,1]} $[0,1]$ .[3]

Subseturi

Dacă ne uităm la setul A = { a , b } {\displaystyle A=\{a,b\}} $A=\{a,b\}$ și setul B = { a , b , c , d } {\displaystyle B=\{a,b,c,d\}} $B=\{a,b,c,d\}$ , se poate observa că toate elementele din primul set se regăsesc și în cel de-al doilea set.
Spunem: { a , b } {\displaystyle \{a,b\}} $\{a,b\}$ este un subset al lui { a , b , c , d } {\displaystyle \{a,b,c,d\}} $\{a,b,c,d\}$
Ca o formulă, arată astfel:
{ a , b } ⊆ $\{a,b\}\subseteq \{a,b,c,d\}$

În general, atunci când toate elementele setului A {\displaystyle A} $A$ sunt, de asemenea, elemente ale setului B {\displaystyle B} $B$ , numim A {\displaystyle A} $A$ un subset al lui B {\displaystyle B} $B$ :
A ⊆ B {\displaystyle A\subseteq B} $A\subseteq B$ . De
obicei se citește " A {\displaystyle A} $A$ este conținut în B {\displaystyle B} $B$ ."

Exemplu: Fiecare Chevrolet este o mașină americană. Așadar, ansamblul tuturor Chevroletelor este conținut în ansamblul tuturor mașinilor americane.

Operațiuni de set

Există diferite moduri de a combina seturile.

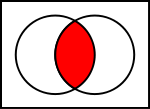
Intersecții

Intersecția A ∩ B {\displaystyle A\cap B} $A\cap B$ a două seturi A {\displaystyle A} $A$ și B {\displaystyle B} $B$ este un set care conține toate elementele care se află atât în setul A {\displaystyle A} $A$ , cât și în setul B {\displaystyle B} $B$ în același timp.

Exemplu: Când A {\displaystyle A} $A$ este ansamblul tuturor mașinilor ieftine, iar B {\displaystyle B} $B$ este ansamblul tuturor mașinilor americane, atunci A ∩ B {\displaystyle A\cap B} $A\cap B$ este ansamblul tuturor mașinilor americane ieftine.

Sindicate

Uniunea A ∪ B {\displaystyle A\cup B} $A\cup B$ a două seturi A {\displaystyle A} $A$ și B {\displaystyle B} $B$ este un set care conține toate elementele care se află în setul A {\displaystyle A} $A$ sau în setul B {\displaystyle B} $B$ . Acest "sau" este o disjuncție inclusivă, astfel încât uniunea conține, de asemenea, elementele care se află în setul A {\displaystyle A} $A$ și în setul B {\displaystyle B} $B$ . Apropo, aceasta înseamnă că intersecția este un subset al uniunii: ( A ∩ B ) ⊆ ( A ∪ $(A\cap B)\subseteq (A\cup B)$ .

Exemplu: Când A {\displaystyle A} $A$ este ansamblul tuturor mașinilor ieftine, iar B {\displaystyle B} $B$ este ansamblul tuturor mașinilor americane, atunci A ∪ B {\displaystyle A\cup B} $A\cup B$ este ansamblul tuturor mașinilor, fără toate mașinile scumpe care nu sunt din America.

Complemente

Complementul poate însemna două lucruri diferite:

Complementul lui A {\displaystyle A} $A$ este universul U {\displaystyle U} $U$ fără toate elementele lui A {\displaystyle A} $A$ :

A C = U ∖ $A^{\rm {C}}=U\setminus A$
Universul U {\displaystyle U} $U$ este ansamblul tuturor lucrurilor despre care vorbiți.
Exemplu: Când U {\displaystyle U} $U$ este ansamblul tuturor mașinilor, iar A {\displaystyle A} $A$ este ansamblul tuturor mașinilor ieftine,
atunci A {\displaystyle A} $A$ ^C este ansamblul tuturor mașinilor scumpe.

Diferența dintre A {\displaystyle A} $A$ și B {\displaystyle B} $B$ este ansamblul B {\displaystyle B} $B$ fără toate elementele din A {\displaystyle A} $A$ :

B ∖ A {\displaystyle B\setminus A} $B\setminus A$
Se mai numește și complementul relativ al lui A {\displaystyle A} $A$ în B {\displaystyle B} $B$ .
Exemplu: Când A {\displaystyle A} $A$ este ansamblul tuturor mașinilor ieftine, iar B {\displaystyle B} $B$ este ansamblul tuturor mașinilor americane, atunci B ∖ A {\displaystyle B\setminus A} $B\setminus A$ este ansamblul tuturor mașinilor americane scumpe.

Dacă schimbați seturile în setul diferență, rezultatul este diferit:
În exemplul cu mașinile, diferența A ∖ B {\displaystyle A\setminus B} $A\setminus B$ este setul tuturor mașinilor ieftine, care nu sunt fabricate în America.

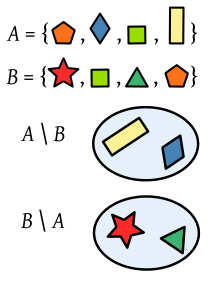
Diferențele dintre două seturi de poligoane

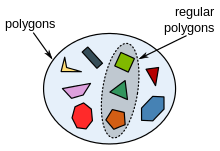
Un subset de poligoane regulate

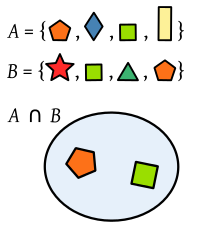
Intersecția a două seturi de poligoane

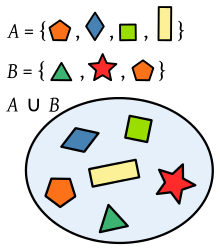
Uniunea a două seturi de poligoane

Notație

Majoritatea matematicienilor folosesc litere ITALICE majuscule (de obicei romane) pentru a scrie despre seturi (cum ar fi A {\displaystyle A} $A$ , B {\displaystyle B} $B$ , C {\displaystyle C} $C$ ). Lucrurile care sunt văzute ca elemente ale seturilor sunt de obicei scrise cu litere romane minuscule.

Un mod de a arăta un set este o listă a membrilor săi, separați prin virgule, incluși între paranteze. De exemplu,

X = { 1 , 2 , 3 } {\displaystyle X=\{1,2,3\}} $X=\{1,2,3\}$ este un set care are membrii 1, 2 și 3.

Un alt mod, numit notația de construire a setului, este prin enunțarea a ceea ce este adevărat pentru membrii setului, astfel:

{x | x este un număr natural & x < 4}.

În limba engleză vorbită, aceasta se citește: "setul tuturor x-urilor astfel încât x este un număr natural și x este mai mic decât patru". Simbolul [ipe "|" înseamnă "astfel încât" sau "astfel încât".

Setul gol se scrie într-un mod special: ∅ {\displaystyle \emptyset } $\emptyset$ , ∅ {\displaystyle \varnothing } $\varnothing$ sau { } {\displaystyle \{\}} {\displaystyle \{\}}. $\{\}$ .

Atunci când obiectul a este membru al setului A {\displaystyle A} $A$ se scrie ca:

$a$ $\in A$ .

În limba engleză vorbită, aceasta se citește: "a este un membru al lui A {\displaystyle A} $A$ ".

Diagrame Venn

Pentru a ilustra operațiile asupra seturilor, matematicienii folosesc diagramele Venn. Diagramele Venn utilizează cercuri pentru a arăta seturile individuale. Universul este reprezentat cu un dreptunghi. Rezultatele operațiilor sunt reprezentate ca zone colorate. În ilustrația operației de intersecție, cercul din stânga arată setul A {\displaystyle A} $A$ și cercul din dreapta arată setul B {\displaystyle B} $B$ .

Intersecție A ∩ B {\displaystyle A\cap B} $A\cap B$

Seturi speciale

Unele seturi sunt foarte importante pentru matematică. Ele sunt utilizate foarte des. Unul dintre acestea este setul gol. Multe dintre aceste seturi speciale se scriu folosind caractere de tip tablă cu bold, iar printre acestea se numără:

P {\displaystyle \mathbb {P} } $\mathbb {P}$ , care reprezintă ansamblul tuturor numerelor prime.
N {\displaystyle \mathbb {N} } $\mathbb {N}$ , care reprezintă ansamblul tuturor numerelor naturale. Altfel spus, N {\displaystyle \mathbb {N} } $\mathbb {N}$ = {1, 2, 3, ...}, sau uneori N {\displaystyle \mathbb {N} } $\mathbb {N}$ = {0, 1, 2, 3, ...}.
Z {\displaystyle \mathbb {Z} } $\mathbb {Z}$ , care reprezintă ansamblul tuturor numerelor întregi (pozitive, negative sau zero). Așadar, Z {\displaystyle \mathbb {Z} } $\mathbb {Z}$ = {..., -2, -1, 0, 1, 2, ...}.
Q {\displaystyle \mathbb {Q} } $\mathbb {Q}$ , care reprezintă ansamblul tuturor numerelor raționale (adică ansamblul tuturor fracțiilor proprii și improprii). Așadar, Q = { a b | a , b ∈ Z , b ≠ 0 } {\displaystyle \mathbb {Q} =\left\{{\begin{matrix}{\frac {a}{b}}}\end{matrix}}|a,b\în \mathbb {Z} ,b\neq 0\right\}} $\mathbb {Q} =\left\{{\begin{matrix}{\frac {a}{b}}\end{matrix}}|a,b\in \mathbb {Z} ,b\neq 0\right\}$ , adică toate fracțiile a b {\displaystyle {\begin{matrix}{\frac {a}{b}}}\end{matrix}}} ${\begin{matrix}{\frac {a}{b}}\end{matrix}}$ unde a și b se află în setul tuturor numerelor întregi și b nu este egal cu 0. De exemplu, 1 4 ∈ Q {\displaystyle {\begin{matrix}{\frac {1}{4}}\end{matrix}}\în \mathbb {Q} } ${\begin{matrix}{\frac {1}{4}}\end{matrix}}\in \mathbb {Q}$ și 11 6 ∈ Q {\displaystyle {\begin{matrix}{\frac {11}{6}}\end{matrix}}}\în \mathbb {Q}. } ${\begin{matrix}{\frac {11}{6}}\end{matrix}}\in \mathbb {Q}$ . Toate numerele întregi se află în acest set, deoarece fiecare număr întreg a poate fi exprimat ca fracția a 1 {\displaystyle {\begin{matrix}{\frac {a}{1}}}\end{matrix}}} ${\begin{matrix}{\frac {a}{1}}\end{matrix}}$ .
R {\displaystyle \mathbb {R} } $\mathbb {R}$ , care reprezintă ansamblul tuturor numerelor reale. Acest set include toate numerele raționale, împreună cu toate numerele iraționale (adică numerele care nu pot fi rescrise ca fracții, cum ar fi π , {\displaystyle \pi ,} $\pi ,$ e , {\displaystyle e,} $e,$ și √2).
C {\displaystyle \mathbb {C} } $\mathbb {C}$ , care reprezintă ansamblul tuturor numerelor complexe.

Fiecare dintre aceste seturi de numere are un număr infinit de elemente, iar P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ $\mathbb {P} \subset \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C}$ .

Paradoxuri despre seturi

Matematicianul Bertrand Russell a constatat că există probleme în ceea ce privește definiția informală a seturilor. El a afirmat acest lucru într-un paradox numit paradoxul lui Russell. O versiune mai ușor de înțeles, mai apropiată de viața reală, se numește paradoxul Barber.

Paradoxul frizerului

Există un orășel pe undeva. În acel oraș, există un frizer. Tuturor bărbaților din oraș nu le place barba, așa că fie se bărbieresc singuri, fie merg la frizerie pentru a fi bărbieriți de către bărbier.

Prin urmare, putem face o afirmație despre bărbierul însuși: Bărbierul rade toți oamenii care nu se rad singuri. El îi bărbierește doar pe acei bărbați (deoarece ceilalți se bărbieresc singuri și nu au nevoie de un bărbier care să le facă bărbieritul).

Acest lucru ridică, desigur, întrebarea: Ce face frizerul în fiecare dimineață pentru a arăta bine bărbierit? Acesta este paradoxul.

Dacă frizerul se rade singur, nu poate fi frizer, deoarece un frizer nu se rade singur. Dacă nu se bărbierește singur, intră în categoria celor care nu se bărbieresc singuri și, prin urmare, nu poate fi frizer.

Pagini conexe

Setul Cantor
Teoria grupurilor
Set deschis
Relația
Teoria seturilor

Întrebări și răspunsuri

Î: Ce este un set?

R: Un set este o idee din matematică. Acesta este format din membri (numiți și elemente) care sunt definiți de membrii lor, astfel încât orice două seturi cu aceiași membri sunt identice.

Î: Poate un set să aibă același membru de mai multe ori?

R: Nu, un set nu poate avea același membru de mai multe ori.

Î: Ordinea contează într-un set?

R: Nu, ordinea nu contează într-un set. Orice lucru poate fi membru al unui set, inclusiv seturile însele.

Î: Ce se întâmplă dacă un set este un membru al lui însuși?

R: Dacă un set este membru al lui însuși, se pot produce paradoxuri precum paradoxul lui Russell.

Î: Este apartenența singurul lucru care contează pentru seturi?

R: Da, apartenența este singurul lucru care contează pentru seturi.

Î: Cum se poate ști dacă două seturi sunt egale?

R: Două seturi sunt egale dacă au aceiași membri.