Matematică

Matematica este studiul numerelor, al formelor și al modelelor. Cuvântul provine din cuvântul grecesc "μάθημα" (máthema), care înseamnă "știință, cunoaștere sau învățare", și este uneori prescurtat în maths (în Anglia, Australia, Irlanda și Noua Zeelandă) sau math (în Statele Unite și Canada). Cuvintele scurte sunt adesea folosite pentru aritmetică, geometrie sau algebră simplă de către elevi și școlile lor.

Matematica include studiul:

Numerele: cum pot fi numărate lucrurile.
Structura: modul în care sunt organizate lucrurile. Acest subdomeniu se numește de obicei algebră.
Loc: locul în care se află lucrurile și dispunerea lor. Acest subdomeniu se numește de obicei geometrie.
Schimbarea: cum se schimbă lucrurile. Acest subdomeniu se numește de obicei analiză.

Matematica este utilă pentru rezolvarea problemelor care apar în lumea reală, astfel încât mulți oameni, în afară de matematicieni, studiază și folosesc matematica. În prezent, matematica este necesară în multe locuri de muncă. Oamenii care lucrează în afaceri, știință, inginerie și construcții au nevoie de cunoștințe de matematică.

Rezolvarea problemelor în matematică

Matematica rezolvă problemele prin utilizarea logicii. Unul dintre principalele instrumente de logică utilizate de matematicieni este deducția. Deducția este un mod special de gândire pentru a descoperi și a demonstra adevăruri noi folosind adevăruri vechi. Pentru un matematician, motivul pentru care un lucru este adevărat (numit dovadă) este la fel de important ca și faptul că este adevărat, iar acest motiv este adesea găsit cu ajutorul deducției. Utilizarea deducției este ceea ce face ca gândirea matematică să fie diferită de alte tipuri de gândire științifică, care s-ar putea baza pe experimente sau pe interviuri.

Logica și raționamentul sunt folosite de matematicieni pentru a crea reguli generale, care reprezintă o parte importantă a matematicii. Aceste reguli omit informațiile care nu sunt importante, astfel încât o singură regulă poate acoperi mai multe situații. Prin găsirea unor reguli generale, matematica rezolvă mai multe probleme în același timp, deoarece aceste reguli pot fi folosite la alte probleme. Aceste reguli pot fi numite teoreme (dacă au fost demonstrate) sau conjecturi (dacă nu se știe încă dacă sunt adevărate). Majoritatea matematicienilor folosesc raționamente non-logice și creative pentru a găsi o demonstrație logică.

Uneori, matematica găsește și studiază reguli sau idei pe care noi nu le înțelegem încă. Adesea, în matematică, ideile și regulile sunt alese pentru că sunt considerate simple sau îngrijite. Pe de altă parte, uneori, aceste idei și reguli sunt găsite în lumea reală după ce sunt studiate în matematică; acest lucru s-a întâmplat de multe ori în trecut. În general, studierea regulilor și ideilor din matematică ne poate ajuta să înțelegem mai bine lumea. Câteva exemple de probleme de matematică sunt adunarea, scăderea, înmulțirea, împărțirea, calculul, fracțiile și zecimalele. Problemele de algebră se rezolvă prin evaluarea anumitor variabile. Un calculator răspunde la fiecare problemă de matematică în cele patru operații aritmetice de bază.

Domenii de studiu în matematică

Număr

Matematica include studiul numerelor și al cantităților.Este o ramură a științei care se ocupă cu logica formei, a cantității și a aranjamentului. Majoritatea domeniilor enumerate mai jos sunt studiate în multe domenii diferite ale matematicii, inclusiv teoria seturilor și logica matematică. Studiul teoriei numerelor se concentrează, de obicei, mai mult pe structura și comportamentul numerelor întregi decât pe fundamentele reale ale numerelor în sine și, prin urmare, nu este enumerat în această subsecțiune.

0 , 1 , 1 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , 1 , ... {\displaystyle \ldots ,-1,0,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0.125 , ... {\displaystyle {\frac {1}{2}},{\frac {2}{3}},0.125,\ldots } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Numere naturale	Întregi	Numere raționale	Numere reale	Numere complexe
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,\div } $+,-,\times ,\div$	> , ≥ , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}}}} $f(x)={\sqrt {x}}$
Numere ordinale	Numere cardinale	Operații aritmetice	Relații aritmetice	Funcții

Structura

Multe domenii ale matematicii studiază structura pe care o are un obiect. Cele mai multe dintre aceste domenii fac parte din studiul algebrei.


Teoria numerelor	Algebră abstractă	Algebră liniară	Teoria ordinii	Teoria grafurilor

Formă

Unele domenii ale matematicii studiază formele lucrurilor. Cele mai multe dintre aceste domenii fac parte din studiul geometriei.


Topologie	Geometrie	Trigonometrie	Geometrie diferențială	Geometrie fractală

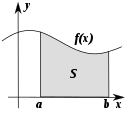
Schimbare

Unele domenii ale matematicii studiază modul în care se schimbă lucrurile. Cele mai multe dintre aceste domenii fac parte din studiul analizei.


Calculul	Calculul vectorial	Analiză

Ecuații diferențiale	Sisteme dinamice	Teoria haosului

Matematică aplicată

Matematica aplicată utilizează matematica pentru a rezolva probleme din alte domenii, cum ar fi ingineria, fizica și informatica.

Analiză numerică - Optimizare - Teoria probabilităților - Statistică - Finanțe matematice - Teoria jocurilor - Fizică matematică - Dinamica fluidelor - Algoritmi computaționali

Teoreme celebre

Aceste teoreme i-au interesat atât pe matematicieni, cât și pe cei care nu sunt matematicieni.

Teorema lui Pitagora - Ultima teoremă a lui Fermat - Conjectura lui Goldbach - Conjectura primilor gemeni - Teoremele de incompletitudine ale lui Gödel - Conjectura lui Poincaré - Argumentul diagonal al lui Cantor - Teorema celor patru culori - Lema lui Zorn - Identitatea lui Euler - Teza Church-Turing

Acestea sunt teoreme și conjecturi care au schimbat foarte mult matematica.

Ipoteza lui Riemann - Ipoteza continuului - P versus NP - Teorema lui Pitagora - Teorema limitei centrale - Teorema fundamentală a calculului - Teorema fundamentală a algebrei - Teorema fundamentală a aritmeticii - Teorema fundamentală a geometriei proiective - Teoreme de clasificare a suprafețelor - Teorema Gauss-Bonnet - Ultima teoremă a lui Fermat - Teorema lui Kantorovici

Fundamente și metode

Progresul în înțelegerea naturii matematicii influențează, de asemenea, modul în care matematicienii își studiază materia.

Filosofia matematicii - Intuiționism matematic - Constructivism matematic - Fundamentele matematicii - Teoria seturilor - Logica simbolică - Teoria modelelor - Teoria categoriilor - Logică - Matematică inversă - Tabel de simboluri matematice

Istoria și lumea matematicienilor

Matematica în istorie și istoria matematicii.

Istoria matematicii - Cronologia matematicii - Matematicieni - Medalia Fields - Premiul Abel - Probleme ale Premiului Mileniului (Clay MathPrize) - Uniunea Internațională de Matematică - Concursuri de matematică - Gândire laterală - Matematică și genul

Premii în domeniul matematicii

Nu există un premiu Nobel pentru matematică. Matematicienii pot primi premiul Abel și medalia Fields pentru lucrări importante.

Institutul de Matematică Clay a declarat că va oferi un milion de dolari oricărei persoane care va rezolva una dintre Problemele Premiului Mileniului.

Instrumente matematice

Există multe instrumente care sunt folosite pentru a face matematică sau pentru a găsi răspunsuri la probleme de matematică.

Instrumente mai vechi

Abacus
Oasele lui Napier, rigla de calcul
Rigla și compasul
Calcul mental

Instrumente mai noi

Calculatoare și calculatoare
Limbaje de programare
Sisteme de algebră pe calculator (listare)
Notație prescurtată pe Internet
software de analiză statistică (de exemplu, SPSS)
Limbaj de programare SAS
Limbajul de programare R

Vezi și

Cronologie a femeilor în matematică
Societatea Americană de Matematică
Societatea pentru Matematică Industrială și Aplicată
Proiectul Genealogie Matematică
Clasificare pe subiecte matematice

Întrebări și răspunsuri

Î: Ce este matematica?

R: Matematica este studiul numerelor, al formelor și al modelelor. Cuvântul provine din cuvântul grecesc μάθημα (máthema), care înseamnă "știință, cunoaștere sau învățătură".

Î: Care sunt principalele domenii ale matematicii?

R: Principalele domenii ale matematicii sunt numerele, structura (algebră), locul (geometrie) și schimbarea (analiză).

Î: Cum este folosită matematica în lumea reală?

R: Matematica aplicată este utilă pentru rezolvarea problemelor din lumea reală. Oamenii care lucrează în afaceri, știință, inginerie și construcții folosesc matematica.

Î: Există o versiune prescurtată a cuvântului "matematică"?

R: Da - poate fi prescurtat în "maths" în țările din Commonwealth-ul britanic sau "math" în America de Nord.

Î: Ce înseamnă cuvântul "matematică"?

R: Cuvântul "matematică" provine din cuvântul grecesc μάθημα (máthema), care înseamnă "știință, cunoaștere sau învățătură".

Î: Ce fel de rezolvare de probleme implică matematica aplicată?

R: Matematica aplicată presupune rezolvarea problemelor din lumea reală cu care se confruntă cei care lucrează în afaceri, știință, inginerie și construcții.