Statistici | ramură a matematicii aplicate care se ocupă cu colectarea, organizarea, analiza, citirea și prezentarea datelor
Statistica este o ramură a matematicii aplicate care se ocupă cu colectarea, organizarea, analiza, citirea și prezentarea datelor. Statisticile descriptive realizează rezumate ale datelor. Statistica inferențială face predicții. Statistica ajută la studiul multor alte domenii, cum ar fi știința, medicina, economia, psihologia, politica și marketingul. Cineva care lucrează în domeniul statisticii se numește statistician. Pe lângă faptul că este numele unui domeniu de studiu, cuvântul "statistică" poate însemna, de asemenea, numere care sunt folosite pentru a descrie date sau relații.
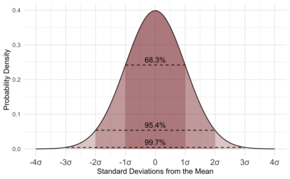
Distribuția normală în statistică
Istoric
Primele statistici cunoscute sunt datele de recensământ. Babilonienii au făcut un recensământ în jurul anului 3500 î.Hr., egiptenii în jurul anului 2500 î.Hr., iar chinezii antici în jurul anului 1000 î.Hr.
Începând cu secolul al XVI-lea, matematicieni precum Gerolamo Cardano au dezvoltat teoria probabilităților, care a făcut din statistică o știință. De atunci, oamenii au colectat și au studiat statisticile cu privire la multe lucruri. Copacii, stelele de mare, stelele, rocile, cuvintele, aproape orice poate fi numărat a fost subiect de statistică.
Colectarea datelor
Înainte de a putea descrie lumea cu ajutorul statisticilor, trebuie să colectăm date. Datele pe care le colectăm în statistică se numesc măsurători. După ce colectăm date, folosim unul sau mai multe numere pentru a descrie fiecare observație sau măsurare. De exemplu, să presupunem că dorim să aflăm cât de populară este o anumită emisiune TV. Putem alege un grup de persoane (numit eșantion) din populația totală de telespectatori. Apoi întrebăm fiecare telespectator din eșantion cât de des se uită la emisiune. Eșantionul reprezintă date pe care le putem vedea, iar populația reprezintă date pe care nu le putem vedea (presupunând că nu toți telespectatorii din populație sunt întrebați). Pentru un alt exemplu, dacă vrem să știm dacă un anumit medicament poate ajuta la scăderea tensiunii arteriale, am putea administra medicamentul respectiv unor persoane pentru o perioadă de timp și am putea măsura tensiunea arterială înainte și după.
Statistici descriptive și inferențiale
Numerele care descriu datele care pot fi observate se numesc statistici descriptive. Numerele care fac predicții despre datele care nu pot fi observate se numesc statistici inferențiale.
Statistica descriptivă presupune utilizarea numerelor pentru a descrie caracteristicile datelor. De exemplu, înălțimea medie a femeilor din Statele Unite este o statistică descriptivă: descrie o caracteristică (înălțimea medie) a unei populații (femeile din Statele Unite).
Odată ce rezultatele au fost rezumate și descrise, acestea pot fi utilizate pentru predicție. Acest lucru se numește statistică inferențială. De exemplu, mărimea unui animal depinde de mai mulți factori. Unii dintre acești factori sunt controlați de mediu, dar alții sunt controlați prin moștenire. Prin urmare, un biolog ar putea elabora un model care să spună că există o probabilitate ridicată ca urmașii să fie de dimensiuni mici - dacă părinții au fost de dimensiuni mici. Acest model permite probabil să prezică dimensiunea în moduri mai bune decât prin simpla ghicire la întâmplare. Testarea faptului dacă un anumit medicament poate fi utilizat pentru a vindeca o anumită afecțiune sau boală se face de obicei prin compararea rezultatelor persoanelor cărora li se administrează medicamentul cu cele cărora li se administrează un placebo.
Metode
Cel mai adesea, colectăm date statistice prin sondaje sau experimente. De exemplu, un sondaj de opinie este un tip de sondaj. Alegem un număr mic de persoane și le punem întrebări. Apoi, folosim răspunsurile lor ca date.
Alegerea persoanelor care vor fi luate pentru un sondaj sau o colectare de date este importantă, deoarece influențează direct statisticile. Atunci când statisticile sunt realizate, nu se mai poate stabili ce persoane sunt luate. Să presupunem că dorim să măsurăm calitatea apei unui lac mare. Dacă luăm probe lângă canalul de scurgere a deșeurilor, vom obține rezultate diferite decât dacă probele sunt luate într-un loc îndepărtat și greu accesibil al lacului.
Există două tipuri de probleme care se întâlnesc frecvent la prelevarea de probe:
- În cazul în care există multe eșantioane, acestea vor fi probabil foarte apropiate de ceea ce sunt în populația reală. Cu toate acestea, dacă există foarte puține eșantioane, este posibil ca acestea să fie foarte diferite de ceea ce sunt în populația reală. Această eroare se numește eroare întâmplătoare (a se vedea și Erori și reziduuri în statistică).
- Persoanele pentru eșantioane trebuie să fie alese cu grijă. De obicei, acestea vor fi alese la întâmplare. În caz contrar, eșantioanele ar putea fi foarte diferite de ceea ce sunt în realitate în populația totală. Acest lucru este valabil chiar dacă se ia un număr mare de eșantioane. Acest tip de eroare se numește distorsiune.
Erori
Putem reduce erorile de șansă prin luarea unui eșantion mai mare și putem evita unele prejudecăți prin alegerea aleatorie. Cu toate acestea, uneori este dificil să se ia eșantioane aleatorii mari. Iar distorsiunea poate apărea dacă diferite persoane nu sunt întrebate sau refuză să răspundă la întrebările noastre sau dacă știu că primesc un tratament fals. Aceste probleme pot fi greu de rezolvat. Consultați eroarea standard pentru mai multe informații.
Statistici descriptive
Găsirea mijlocului de date
Mijlocul datelor se numește medie. Media ne vorbește despre un individ tipic din populație. Există trei tipuri de medii care sunt adesea utilizate: media, mediana și modul.
Exemplele de mai jos utilizează aceste date de probă:
| Nume | A | B | C | D | E | F | G | H | I | J |
| Scor | 23 | 26 | 49 | 49 | 57 | 64 | 66 | 78 | 82 | 92 |
Medie
Formula pentru medie este
Unde 

Aceasta înseamnă că se calculează media prin însumarea tuturor valorilor, apoi se împarte la numărul de valori. Pentru exemplul de mai sus, media este:
Problema cu media este că aceasta nu ne spune nimic despre modul în care sunt distribuite valorile. Valorile care sunt foarte mari sau foarte mici modifică foarte mult media. În statistică, aceste valori extreme pot fi erori de măsurare, dar uneori populația conține într-adevăr aceste valori. De exemplu, dacă într-o cameră sunt 10 persoane care câștigă 10 dolari pe zi și una care câștigă 1.000.000 de dolari pe zi. Media datelor este de 90.918 dolari pe zi. Chiar dacă este suma medie, media în acest caz nu reprezintă suma pe care o câștigă o singură persoană și, prin urmare, nu este foarte utilă în anumite scopuri.
Media descrisă mai sus este "media aritmetică". Alte tipuri sunt utile în anumite scopuri.
Mediană
Mediana este elementul de mijloc al datelor. Pentru o anumită dată de date 

Ca un alt exemplu, la fel ca exemplul venitului prezentat pentru medie, luați în considerare o cameră cu 10 persoane care au venituri de 10, 20, 20, 20, 40, 50, 50, 60, 90, 90, 90, 100 și 1.000.000 de dolari. Aici, mediana este de 55 $, deoarece 55 $ este media celor două numere de mijloc, 50 $ și 60 $. Dacă se ignoră valoarea extremă de 1.000.000 $, media este de 53 $. În acest caz, mediana este apropiată de valoarea obținută atunci când valoarea extremă este eliminată. Mediana rezolvă problema valorilor extreme, așa cum este descrisă în definiția mediei de mai sus.
Mod
Modul este cel mai frecvent element de date. De exemplu, cea mai frecventă literă din limba engleză este litera "e". Am putea spune că "e" este modul de distribuție a literelor.
Ca un alt exemplu, dacă într-o cameră se află 10 persoane cu venituri de 10, 20, 20, 20, 40, 50, 60, 90, 90, 90, 90, 90, 100 și 1.000.000 de dolari, atunci modul este 90 de dolari, deoarece 90 de dolari apare de trei ori și toate celelalte valori apar de mai puțin de trei ori.
Poate exista mai mult de un mod. De exemplu, dacă într-o cameră se află 10 persoane cu venituri de 10$, 20$, 20$, 20$, 20$, 50$, 60$, 90$, 90$, 90$, 100$ și 1.000.000$, modurile sunt 20$ și 90$. Acest lucru este bi-modal, sau are două moduri. Bi-modalitatea este foarte frecventă și indică adesea faptul că datele sunt combinația a două grupuri diferite. De exemplu, înălțimea medie a tuturor adulților din SUA are o distribuție bi-modală. Acest lucru se datorează faptului că bărbații și femeile au înălțimi medii separate de 1,763 m (5 ft 9 + 1⁄2 in) pentru bărbați și 1,622 m (5 ft 4 in) pentru femei. Aceste vârfuri sunt evidente atunci când ambele grupuri sunt combinate.
Modul este singura formă de medie care poate fi utilizată pentru datele care nu pot fi puse în ordine.
Găsirea răspândirii datelor
Un alt lucru pe care îl putem spune despre un set de date este cât de împrăștiate sunt acestea. Un mod obișnuit de a descrie răspândirea unui set de date este deviația standard. Dacă deviația standard a unui set de date este mică, atunci majoritatea datelor sunt foarte apropiate de medie. Dacă deviația standard este mare, însă, atunci o mare parte din date sunt foarte diferite de medie.
Abaterea standard a unui eșantion este, în general, diferită de abaterea standard a populației sale de origine. Din acest motiv, scriem 

În cazul în care datele urmează modelul comun numit distribuție normală, atunci este foarte util să se cunoască abaterea standard. Dacă datele urmează acest model (am spune că datele sunt distribuite în mod normal), aproximativ 68 din 100 de date se vor abate de la medie cu o valoare mai mică decât abaterea standard. Nu numai atât, dar aproximativ 95 din fiecare 100 de măsurători vor fi în afara mediei cu mai puțin de două ori deviația standard, iar aproximativ 997 din 1000 vor fi mai aproape de medie cu mai puțin de trei deviații standard.
Alte statistici descriptive
De asemenea, putem folosi statisticile pentru a afla că un anumit procent, percentila, număr sau fracțiune de persoane sau lucruri dintr-un grup fac ceva sau se încadrează într-o anumită categorie.
De exemplu, oamenii de știință din domeniul social au folosit statisticile pentru a descoperi că 49% dintre oamenii din lume sunt bărbați.
Softuri conexe
Pentru a veni în sprijinul statisticienilor, au fost dezvoltate numeroase programe statistice:
- MATLAB
- R
- Institutul SAS
- SPSS (realizat de IBM)
Întrebări și răspunsuri
Î: Ce este statistica?
R: Statistica este o ramură a matematicii aplicate care se ocupă cu colectarea, organizarea, analiza, citirea și prezentarea datelor.
Î: Care sunt cele două tipuri de statistici?
R: Cele două tipuri de statistici sunt cele descriptive și cele inferențiale. Statisticile descriptive fac rezumate ale datelor, în timp ce statisticile inferențiale fac predicții.
Î: Cum ajută statistica în alte domenii?
R: Statistica ajută la studiul multor alte domenii, cum ar fi știința, medicina, economia, psihologia, politica și marketingul.
Î: Cine lucrează în domeniul statisticii?
R: Cineva care lucrează în domeniul statisticii se numește statistician.
Î: Ce înseamnă cuvântul "statistică"?
R: Pe lângă faptul că este numele unui domeniu de studiu, cuvântul "statistică" poate însemna, de asemenea, numere care sunt folosite pentru a descrie date sau relații.
Î: Care sunt activitățile pe care le desfășoară statisticienii?
R: Statisticienii se angajează în activități precum colectarea, organizarea, analiza, citirea și prezentarea datelor.
Căuta în

