Abatere standard | un număr utilizat pentru a indica modul în care măsurătorile pentru un grup sunt dispersate față de medie
Abaterea standard este un număr utilizat pentru a indica modul în care măsurătorile unui grup sunt dispersate față de medie (media sau valoarea așteptată). O abatere standard scăzută înseamnă că majoritatea cifrelor sunt apropiate de medie, în timp ce o abatere standard ridicată înseamnă că cifrele sunt mai dispersate.
Marja de eroare raportată este, de obicei, de două ori mai mare decât abaterea standard. Oamenii de știință raportează în mod obișnuit abaterea standard a numerelor de la numărul mediu în experimente. Aceștia decid adesea că numai diferențele mai mari decât de două sau trei ori deviația standard sunt importante. Deviația standard este, de asemenea, utilă în domeniul monetar, unde deviația standard a dobânzii câștigate arată cât de diferită poate fi dobânda câștigată de o persoană față de medie.
De multe ori, poate fi măsurat doar un eșantion sau o parte a unui grup. Atunci se poate găsi un număr apropiat de abaterea standard pentru întregul grup printr-o ecuație ușor diferită, numită abaterea standard a eșantionului, explicată mai jos. În acest caz, abaterea standard a întregului grup este reprezentată de litera greacă 

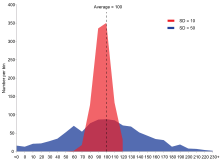
Exemplu de două populații eșantionate cu aceeași medie și deviații standard diferite. Populația roșie are media 100 și abaterea standard 10; populația albastră are media 100 și abaterea standard 50.
.png)
Un grafic al unei distribuții normale (sau curbă în clopot). Fiecare bandă colorată are o lățime de o abatere standard.
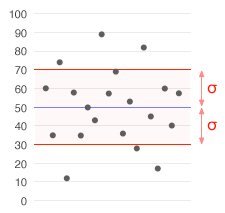
Un set de date cu o medie de 50 (reprezentată în albastru) și o abatere standard (σ) de 20.
Exemplu de bază
Să considerăm un grup care are următoarele opt numere:
Aceste opt numere au media (media) de 5:
Pentru a calcula abaterea standard a populației, găsiți mai întâi diferența dintre fiecare număr din listă și medie. Apoi, ridicați la pătrat rezultatul fiecărei diferențe:
Apoi, găsiți media acestor valori (suma împărțită la numărul de numere). În cele din urmă, luați rădăcina pătrată:
Răspunsul este abaterea standard a populației. Formula este adevărată doar dacă cele opt numere cu care am început reprezintă întregul grup. Dacă acestea reprezintă doar o parte a grupului ales la întâmplare, atunci putem obține o estimare nepărtinitoare a deviației standard a populației prin împărțirea la 7 (care este n - 1) în loc de 8 (care este n) în partea de jos (numitorul) a formulei de mai sus. Răspunsul este atunci abaterea standard a eșantionului (corectată în funcție de bias). Aceasta se numește corecția lui Bessel. Utilizăm adesea această corecție deoarece varianța eșantionului, adică pătratul abaterii standard a eșantionului, este un estimator nepărtinitor al varianței populației, cu alte cuvinte, valoarea așteptată sau media pe termen lung a varianței eșantionului este egală cu varianța (adevărată) a populației. Cu toate acestea, nu este cazul ca abaterea standard a eșantionului să fie un estimator imparțial al abaterii standard a populației[1].[1] Deși corecția lui Bessel este o estimare imparțială a varianței, această estimare are o eroare medie pătratică mai mare decât estimarea părtinitoare sau, cu alte cuvinte, estimarea părtinitoare (adică împărțind la n și nu la n-1) este în medie mai aproape de valoarea reală.
Mai multe exemple
Iată un exemplu ceva mai greu, din viața reală: Înălțimea medie a bărbaților adulți din Statele Unite este de 70", cu o deviație standard de 3". O abatere standard de 3" înseamnă că majoritatea bărbaților (aproximativ 68%, presupunând o distribuție normală) au o înălțime cu 3" mai înaltă până la 3" mai mică decât media (67"-73") - o abatere standard. Aproape toți bărbații (aproximativ 95%) au o înălțime cu 6" mai înaltă până la 6" mai scurtă decât media (64"-76") - două abateri standard. Trei abateri standard includ toate cifrele pentru 99,7% din populația eșantionului studiat. Acest lucru este valabil dacă distribuția este normală (în formă de clopot).
Dacă deviația standard ar fi zero, atunci toți bărbații ar avea exact 70" înălțime. Dacă abaterea standard ar fi de 20", atunci unii bărbați ar fi mult mai înalți sau mult mai scunzi decât media, cu un interval tipic de aproximativ 50"-90".
Pentru un alt exemplu, fiecare dintre cele trei grupuri {0, 0, 14, 14}, {0, 6, 8, 14} și {6, 6, 8, 8} are o medie (medie) de 7. Dar abaterile lor standard sunt 7, 5 și 1. Cel de-al treilea grup are o abatere standard mult mai mică decât celelalte două, deoarece numerele sale sunt toate apropiate de 7. În general, abaterea standard ne spune cât de departe de medie tind să fie restul numerelor și va avea aceleași unități ca și numerele în sine. Dacă, de exemplu, grupul {0, 6, 8, 14} reprezintă vârstele unui grup de patru frați în ani, media este de 7 ani, iar abaterea standard este de 5 ani.
Abaterea standard poate servi ca măsură a incertitudinii. În știință, de exemplu, abaterea standard a unui grup de măsurători repetate îi ajută pe oamenii de știință să știe cât de siguri sunt de numărul mediu. Atunci când se decide dacă măsurătorile dintr-un experiment sunt în concordanță cu o predicție, abaterea standard a acestor măsurători este foarte importantă. Dacă numărul mediu din experimente este prea departe de numărul prezis (distanța fiind măsurată în deviații standard), atunci este posibil ca teoria testată să nu fie corectă. Pentru mai multe informații, consultați intervalul de predicție.
Exemple de aplicații
Înțelegerea deviației standard a unui set de valori ne permite să știm cât de mare este diferența față de "medie" (medie).
Vremea
Ca un exemplu simplu, luați în considerare temperaturile medii zilnice maxime pentru două orașe, unul în interiorul țării și unul în apropierea oceanului. Este util să înțelegem că intervalul temperaturilor maxime zilnice pentru orașele din apropierea oceanului este mai mic decât pentru orașele din interiorul țării. Este posibil ca aceste două orașe să aibă fiecare aceeași temperatură medie zilnică ridicată. Cu toate acestea, abaterea standard a temperaturii maxime zilnice pentru orașul de coastă va fi mai mică decât cea a orașului din interiorul țării .
Sport
Un alt mod de a vedea acest lucru este de a lua în considerare echipele sportive. În orice sport, vor exista echipe care se pricep la unele lucruri și nu la altele. Echipele care se clasează pe primele locuri nu vor prezenta prea multe diferențe în ceea ce privește abilitățile. Ele se descurcă bine în majoritatea categoriilor. Cu cât deviația standard a abilităților lor în fiecare categorie este mai mică, cu atât sunt mai echilibrate și mai consecvente. Cu toate acestea, echipele cu o deviație standard mai mare vor fi mai puțin previzibile. O echipă care, de obicei, nu se descurcă bine în majoritatea categoriilor va avea o deviație standard scăzută. O echipă care este de obicei bună în majoritatea categoriilor va avea, de asemenea, o deviație standard scăzută. Cu toate acestea, o echipă cu o deviație standard ridicată ar putea fi genul de echipă care înscrie multe puncte (atac puternic), dar care permite și celeilalte echipe să înscrie multe puncte (apărare slabă).
Încercarea de a ști dinainte care echipe vor câștiga poate include examinarea deviațiilor standard ale diferitelor "statistici" ale echipelor. Numerele care sunt diferite de cele așteptate pot face să se potrivească punctele forte cu cele slabe pentru a arăta care sunt motivele care pot fi cele mai importante pentru a ști ce echipă va câștiga.
În curse, se măsoară timpul necesar unui pilot pentru a termina fiecare tur de pistă. Un pilot cu o abatere standard scăzută a timpilor pe tur este mai constant decât un pilot cu o abatere standard mai mare. Aceste informații pot fi folosite pentru a ajuta la înțelegerea modului în care un pilot poate reduce timpul necesar pentru a termina un tur.
Bani
În domeniul monetar, deviația standard poate însemna riscul ca un preț să crească sau să scadă (acțiuni, obligațiuni, proprietăți etc.). Poate însemna, de asemenea, riscul ca un grup de prețuri să crească sau să scadă (fonduri mutuale gestionate activ, fonduri mutuale indexate sau ETF-uri). Riscul este un motiv pentru a lua decizii cu privire la ce să cumperi. Riscul este un număr pe care oamenii îl pot folosi pentru a ști câți bani pot câștiga sau pierde. Pe măsură ce riscul devine mai mare, randamentul unei investiții poate fi mai mare decât cel așteptat (deviația standard "plus"). Cu toate acestea, o investiție poate, de asemenea, să piardă mai mulți bani decât se așteaptă (abaterea standard "în minus").
De exemplu, o persoană trebuia să aleagă între două acțiuni. Acțiunea A a avut în ultimii 20 de ani un randament mediu de 10 %, cu o deviație standard de 20 de puncte procentuale (pp). Acțiunea B a avut în ultimii 20 de ani un randament mediu de 12%, dar o deviație standard mai mare, de 30 pp. Gândindu-se la risc, persoana poate decide că stocul A este cea mai sigură alegere. Chiar dacă s-ar putea să nu câștige la fel de mulți bani, probabil că nici nu va pierde prea mulți bani. Persoana poate crede că media mai mare cu 2 puncte a acțiunii B nu merită abaterea standard suplimentară de 10 pp (risc mai mare sau incertitudine a randamentului așteptat).
Reguli pentru numere distribuite normal
Majoritatea ecuațiilor matematice pentru abaterea standard presupun că numerele sunt distribuite normal. Acest lucru înseamnă că numerele sunt răspândite într-un anumit mod pe ambele părți ale valorii medii. Distribuția normală se mai numește și distribuție gaussiană, deoarece a fost descoperită de Carl Friedrich Gauss. Este adesea numită curba clopotului, deoarece numerele se distribuie pentru a avea forma unui clopot pe un grafic.
Numerele nu sunt distribuite în mod normal dacă sunt grupate de o parte sau de cealaltă a valorii medii. Numerele pot fi împrăștiate și totuși să fie distribuite normal. Abaterea standard arată cât de mult sunt răspândite numerele.

Albastrul închis reprezintă mai puțin de o abatere standard de la medie. Pentru distribuția normală, aceasta include 68,27% din numere; în timp ce două abateri standard de la medie (albastru mediu și albastru închis) includ 95,45%; trei abateri standard (albastru deschis, mediu și închis) includ 99,73%; iar patru abateri standard reprezintă 99,994%.
Relația dintre medie (medie) și abaterea standard
Media (media) și abaterea standard a unui set de date sunt de obicei scrise împreună. Astfel, o persoană poate înțelege care este numărul mediu și cât de mult sunt răspândite celelalte numere din grup.
Modul în care este distribuit un grup de numere poate fi, de asemenea, dat de coeficientul de variație (CV), care reprezintă abaterea standard împărțită la medie. Acesta este un număr adimensional. Coeficientul de variație este adesea înmulțit cu 100% și scris ca procent.
Istoric
Termenul de abatere standard a fost folosit pentru prima dată în scris de Karl Pearson în 1894, după ce l-a folosit în cadrul unor cursuri. Acesta a fost ca un înlocuitor pentru denumirile anterioare pentru aceeași idee: de exemplu, Gauss folosea eroarea medie.
Pagini conexe
- Acuratețe și precizie
- Dimensiunea eșantionului
- Eroare standard
- Variație
Întrebări și răspunsuri
Î: Ce este abaterea standard?
R: Abaterea standard este un număr utilizat pentru a indica modul în care măsurătorile unui grup sunt dispersate față de medie (media sau valoarea așteptată).
Î: Ce înseamnă o deviație standard scăzută?
R: O abatere standard scăzută înseamnă că majoritatea numerelor sunt apropiate de medie.
Î: Ce înseamnă o abatere standard ridicată?
R: O deviație standard ridicată înseamnă că numerele sunt mai dispersate.
Î: Cum se utilizează abaterea standard în bani?
R: În domeniul monetar, abaterea standard a dobânzii obținute arată cât de diferită poate fi dobânda obținută de o persoană față de medie.
Î: Când poate fi măsurată doar o parte a unui grup?
R: De multe ori, poate fi măsurat doar un eșantion sau o parte a unui grup.
Î: Cum este reprezentată abaterea standard a întregului grup?
R: Abaterea standard a întregului grup este reprezentată de litera greacă َ {\displaystyle \sigma }. .
Î: Cum este reprezentată abaterea standard a eșantionului?
R: Deviația standard a eșantionului este reprezentată de s {\displaystyle s} .
Căuta în



