Teoria grafurilor | un domeniu al matematicii despre grafuri
Teoria grafurilor este un domeniu al matematicii despre grafuri. Un grafic este o reprezentare abstractă a: unui număr de puncte care sunt conectate prin linii. Fiecare punct se numește, de obicei, un vertex (mai multe puncte se numesc vertexuri), iar liniile se numesc muchii. Grafurile sunt un instrument de modelare a relațiilor. Ele sunt utilizate pentru a găsi răspunsuri la o serie de probleme.
Unele dintre aceste întrebări sunt:
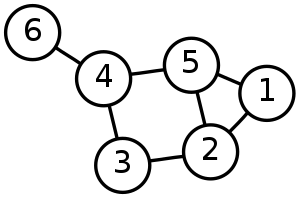
Un graf neorientat.
Diferite tipuri de grafuri
- Teoria grafurilor are multe aspecte. Grafurile pot fi direcționate sau nedirecționate. Un exemplu de graf dirijat ar fi sistemul de drumuri dintr-un oraș. Unele străzi din oraș sunt străzi cu sens unic. Acest lucru înseamnă că pe acele porțiuni există o singură direcție de urmat.
- Graficele pot fi ponderate. Un exemplu ar fi o rețea rutieră, cu distanțe sau cu taxe de drum (pentru drumuri).
- Nodurile (cercurile din schemă) unui graf se numesc vertici. Liniile care leagă nodurile se numesc muchii. Între două noduri nu poate exista nicio linie, poate exista o singură linie sau pot exista mai multe linii.
- În teoria grafurilor, structurile de arbori sunt utilizate pe scară largă, acestea reprezentând structuri ierarhice. Un arbore este un graf dirijat sau nedirijat în care nu există cicluri, ceea ce înseamnă că nu există nicio modalitate de a merge de la un vertex (de exemplu, un oraș) la același vertex folosind fiecare muchie pe care o folosești o singură dată (mergând o singură dată pe fiecare drum pe care îl parcurgi).
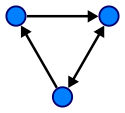
Un graf dirijat.
Istoric
 →
→ →
→ 
O vizualizare a celor șapte poduri de la Königberg. Leonhard Euler a rezolvat această problemă în 1736, ceea ce a dus la dezvoltarea topologiei și a teoriei moderne a grafurilor.
Un graf este o structură de date abstractă. Acesta conține noduri care sunt, de obicei, legate între ele. Un nod este un set de date, de obicei sub forma unor perechi ordonate. Nodurile sunt fie conectate, fie neconectate cu un alt nod. Relația dintre noduri este de obicei definită ca o muchie. Grafurile sunt utile pentru capacitatea lor de a asocia noduri cu alte noduri. În practică, există câteva reprezentări ale grafurilor.
Leonhard Euler locuia într-un oraș numit Königsberg. (Numele său s-a schimbat în Kaliningrad în 1946). Orașul se află pe râul Pregel. Există o insulă în râu. Există câteva poduri peste râu. Euler a vrut să se plimbe și să folosească o dată fiecare dintre poduri. El a întrebat dacă poate face acest lucru. În 1736, a publicat un articol științific în care a arătat că acest lucru nu este posibil. Astăzi, această problemă este cunoscută sub numele de "Cele șapte poduri din Königsberg". Articolul este considerat ca fiind primul articol din istoria teoriei grafurilor.
Acest articol, ca și cel scris de Vandermonde despre problema cavalerului, a continuat analiza situs inițiată de Leibniz. Formula lui Euler privind numărul de muchii, vârfuri și fețe ale unui poliedru convex a fost studiată și generalizată de Cauchy și L'Huillier și se află la originea topologiei.
Fuziunea ideilor provenite din matematică cu cele din chimie se află la originea unei părți din terminologia standard a teoriei grafurilor. În special, termenul "graf" a fost introdus de Sylvester într-un articol publicat în 1878 în Nature.
Una dintre cele mai faimoase și productive probleme ale teoriei grafurilor este problema celor patru culori: "Este adevărat că orice hartă desenată în plan poate avea regiunile sale colorate cu patru culori, astfel încât două regiuni care au o frontieră comună să aibă culori diferite?".
.png)
Problema podului Königsberg, pe o hartă a orașului
.png)
Aceeași problemă, dar folosind un grafic
Teoria grafurilor în perspectivă
Teoria grafurilor este o parte importantă a matematicii și a informaticii. Pentru multe astfel de probleme există soluții exacte. De multe ori însă, acestea sunt foarte greu de calculat. Prin urmare, foarte des se folosesc aproximări. Există două tipuri de astfel de aproximări, algoritmii Monte-Carlo și algoritmii Las-Vegas.
Pagini conexe
Întrebări și răspunsuri
Î: Ce este teoria grafurilor?
R: Teoria grafurilor este un domeniu al matematicii care studiază grafurile, care sunt reprezentări abstracte ale punctelor conectate prin linii.
Î: Cum se numesc punctele dintr-un grafic?
R: Punctele dintr-un graf sunt denumite, de obicei, vârfuri.
Î: Ce reprezintă liniile dintre vârfuri?
R: Liniile dintre vârfuri reprezintă relații sau conexiuni între ele.
Î: Cum pot fi utilizate graficele?
R: Graficele pot fi utilizate pentru a modela relații și pentru a găsi răspunsuri la diverse probleme.
Î: La ce fel de întrebări pot ajuta graficele să răspundă?
R: Graficele pot ajuta la răspunsuri la întrebări legate de analiza rețelelor, optimizare și programare.
Î: Există diferite tipuri de grafuri?
R: Da, există diferite tipuri de grafuri, cum ar fi grafurile direcționate și nedirecționate, grafurile ponderate și neponderate, grafurile complete și incomplete etc.
Î: Există vreun software disponibil pentru a lucra cu teoria grafurilor?
R: Da, există software disponibil pentru lucrul cu teoria grafurilor, cum ar fi Gephi și NetworkX.
Căuta în