Teorema celor patru culori | Teoremă de matematică
Teorema celor patru culori este o teoremă de matematică. Aceasta spune că în orice suprafață plană cu regiuni (oamenii se gândesc la ele ca la hărți), regiunile pot fi colorate cu cel mult patru culori. Două regiuni care au o graniță comună nu trebuie să primească aceeași culoare. Ele sunt numite adiacente (una lângă cealaltă) dacă au în comun un segment de frontieră, nu doar un punct.
Aceasta a fost prima teoremă demonstrată de un computer, în cadrul unei demonstrații prin epuizare. În cazul demonstrației prin epuizare, concluzia este stabilită prin împărțirea în cazuri și demonstrarea fiecăruia separat. Este posibil să existe o mulțime de cazuri. De exemplu, prima demonstrație a teoremei celor patru culori a fost o demonstrație prin epuizare cu 1.936 de cazuri. Această demonstrație a fost controversată deoarece majoritatea cazurilor au fost verificate de un program de calculator, nu manual. Cea mai scurtă demonstrație cunoscută astăzi a teoremei celor patru culori are încă peste 600 de cazuri.
Chiar dacă problema a fost prezentată inițial ca o problemă de colorare a hărților politice ale țărilor, cartografii nu sunt foarte interesați de ea. Potrivit unui articol al istoricului de matematică Kenneth May (Wilson 2002, 2), "Hărțile care utilizează doar patru culori sunt rare, iar cele care o fac necesită de obicei doar trei. Cărțile despre cartografie și istoria realizării hărților nu menționează proprietatea celor patru culori".
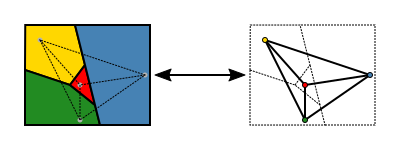
Multe hărți mai simple pot fi colorate folosind trei culori. A patra culoare este necesară pentru unele hărți, cum ar fi cea în care o regiune este înconjurată de un număr impar de altele, care se ating între ele într-un ciclu. Un astfel de exemplu este prezentat în imagine. Teorema celor cinci culori afirmă că cinci culori sunt suficiente pentru a colora o hartă. Ea are o demonstrație scurtă și elementară și a fost demonstrată la sfârșitul secolului al XIX-lea. (Heawood 1890) Demonstrarea faptului că este nevoie doar de patru culori s-a dovedit a fi mult mai dificilă. De la prima enunțare a teoremei celor patru culori, în 1852, au apărut multe dovezi false și contraexemple false.

Exemplu de hartă în patru culori

Trei culori nu sunt suficiente pentru a colora această hartă.
Formularea exactă a problemei
În mod intuitiv, teorema celor patru culori poate fi enunțată astfel: "dată fiind orice împărțire a unui plan în regiuni contigue, numită hartă, regiunile pot fi colorate folosind cel mult patru culori, astfel încât două regiuni adiacente să nu aibă aceeași culoare". Pentru a putea rezolva corect problema, este necesar să clarificăm unele aspecte: În primul rând, trebuie ignorate toate punctele care aparțin la trei sau mai multe țări. În al doilea rând, hărțile bizare cu regiuni de suprafață finită și perimetru infinit pot necesita mai mult de patru culori.
În sensul teoremei, fiecare "țară" trebuie să fie o regiune simplu conectată sau contiguă. În lumea reală, acest lucru nu este adevărat: Alaska, ca parte a Statelor Unite, Nakhchivan, ca parte a Azerbaidjanului, și Kaliningrad, ca parte a Rusiei, nu sunt contigue. Deoarece teritoriul unei anumite țări trebuie să fie de aceeași culoare, patru culori pot fi insuficiente. De exemplu, luați în considerare o hartă simplificată, cum ar fi cea prezentată în stânga: Pe această hartă, cele două regiuni etichetate A aparțin aceleiași țări și trebuie să aibă aceeași culoare. Această hartă are nevoie de cinci culori, deoarece cele două regiuni A împreună sunt contigue cu alte patru regiuni, fiecare dintre acestea fiind contiguă cu toate celelalte. Dacă A ar avea doar trei regiuni, ar putea fi necesare șase sau mai multe culori. În acest fel, este posibil să se realizeze hărți care necesită un număr arbitrar de mare de culori. O construcție similară se aplică și în cazul în care se folosește o singură culoare pentru toate corpurile de apă, așa cum se întâmplă de obicei pe hărțile reale.
O versiune mai ușor de enunțat a teoremei folosește teoria grafurilor. Setul de regiuni ale unei hărți poate fi reprezentat mai abstract ca un graf nedirijat care are un vertex pentru fiecare regiune și o muchie pentru fiecare pereche de regiuni care împart un segment de frontieră. Acest graf este planar: poate fi desenat în plan fără încrucișări prin plasarea fiecărui vârf într-o locație aleasă în mod arbitrar în cadrul regiunii căreia îi corespunde și prin desenarea marginilor sub formă de curbe care conduc fără încrucișări în cadrul fiecărei regiuni de la locația vârfului la fiecare punct de frontieră comun al regiunii. Invers, orice graf planar poate fi format în acest mod dintr-o hartă. În terminologia teoriei grafurilor, teorema celor patru culori afirmă că vârfurile oricărui graf planar pot fi colorate cu cel mult patru culori, astfel încât niciunul dintre cele două vârfuri adiacente să nu aibă aceeași culoare sau, pe scurt, "orice graf planar poate fi colorat cu patru culori" (Thomas 1998, p. 849; Wilson 2002).

Exemplu de hartă a Azerbaidjanului cu regiuni necontinue

Această hartă nu poate fi colorată cu patru culori
Istoric
Prima persoană care a numit problema a fost Francis Guthrie, în 1852. Acesta era student la drept în Anglia, la acea vreme. El a constatat că avea nevoie de cel puțin patru culori pentru a colora o hartă a comitatelor din Anglia. Augustus de Morgan a discutat pentru prima dată despre această problemă într-o scrisoare adresată lui Rowan Hamliton în august 1852. În scrisoare, de Morgan se întreabă dacă patru culori sunt într-adevăr suficiente pentru a colora o hartă, astfel încât țările care se află una lângă alta să aibă culori diferite.
Matematicianul englez Arthur Cayley a prezentat problema în fața societății matematice din Londra, în 1878. În decurs de un an, Alfred Kempe a găsit ceea ce părea a fi o dovadă a problemei. Unsprezece ani mai târziu, în 1890, Percy Heawood a demonstrat că dovada lui Alfred era greșită. Peter Guthrie Tait a prezentat o altă încercare de demonstrație în 1880. A fost nevoie de unsprezece ani pentru a demonstra că nici demonstrația lui Tait nu funcționa. În 1891, Julius Petersen a reușit să demonstreze acest lucru. Atunci când a falsificat demonstrația lui Cayley, Kempe a prezentat și o demonstrație pentru o problemă pe care a numit-o teorema celor cinci culori. Teorema spune că orice astfel de hartă poate fi colorată cu cel mult cinci culori. Există două restricții: În primul rând, orice țară este contiguă, nu există exclave. A doua restricție este că țările trebuie să aibă o graniță comună; dacă se ating doar într-un punct, ele pot fi colorate cu aceeași culoare. Chiar dacă demonstrația lui Kempe a fost greșită, el a folosit unele dintre ideile care vor permite mai târziu o demonstrație corectă.
În anii '60 și '70, Heinrich Heesch a elaborat o primă schiță de demonstrație prin calculator. Kenneth Appel și Wolfgang Haken au îmbunătățit această schiță în 1976 (Robertson et al. 1996). Aceștia au reușit să reducă numărul de cazuri care ar fi trebuit să fie testate la 1936; a fost realizată o versiune ulterioară care se baza pe testarea a doar 1476 de cazuri. Fiecare caz trebuia să fie testat de un computer (Appel & Haken 1977) harv error: multiple targets (2×): CITEREFAppelHaken1977 (ajutor).
În 1996, Neil Robertson, Daniel Sanders, Paul Seymour și Robin Thomas au îmbunătățit metoda și au redus numărul de cazuri care trebuiau testate la 663. Din nou, fiecare caz trebuia să fie testat pe calculator.
În 2005, Georges Gonthier și Benjamin Werner au elaborat o dovadă formală. Aceasta a reprezentat o îmbunătățire, deoarece a permis pentru prima dată utilizarea unui software de rezolvare a teoremelor. Software-ul utilizat se numește Coq.
Teorema celor patru culori este prima mare problemă matematică care a fost demonstrată cu ajutorul unui calculator. Deoarece demonstrația nu poate fi făcută de un om, unii matematicieni nu au recunoscut-o ca fiind corectă. Pentru a verifica demonstrația, este necesar să ne bazăm pe un software și un hardware care funcționează corect pentru a valida demonstrația. Pentru că demonstrația a fost realizată cu ajutorul unui calculator, aceasta nu este, de asemenea, foarte elegantă.
Încercări care s-au dovedit a fi greșite
Teorema celor patru culori este cunoscută pentru faptul că a atras un număr mare de dovezi și infirmări false în lunga sa istorie. La început, The New York Times a refuzat să relateze despre demonstrația lui Appel-Haken. Ziarul a făcut acest lucru ca o chestiune de politică; se temea că demonstrația se va dovedi falsă, ca și cele anterioare (Wilson 2002, p. 209). Unele dovezi au durat mult timp, până când au putut fi falsificate: În cazul dovezilor lui Kempe și Tait, falsificarea lor a durat peste un deceniu.
Cele mai simple contraexemple încearcă, în general, să creeze o regiune care să le atingă pe toate celelalte. Acest lucru forțează regiunile rămase să fie colorate doar cu trei culori. Deoarece teorema celor patru culori este adevărată, acest lucru este întotdeauna posibil; cu toate acestea, deoarece persoana care desenează harta se concentrează asupra unei singure regiuni mari, nu observă că regiunile rămase pot fi, de fapt, colorate cu trei culori.
Acest truc poate fi generalizat: Dacă culorile unor regiuni dintr-o hartă sunt alese în prealabil, devine imposibil să se coloreze restul regiunilor în așa fel încât să se folosească în total doar patru culori. Cineva care verifică contraexemplul s-ar putea să nu se gândească că ar putea fi necesar să schimbe culoarea acestor regiuni. Acest lucru va face ca contraexemplul să pară valid, chiar dacă nu este.
Poate că un efect care stă la baza acestei concepții greșite comune este faptul că restricția de culoare nu este tranzitivă: o regiune trebuie să fie colorată diferit doar de regiunile pe care le atinge direct, nu și de regiunile care ating regiuni pe care le atinge. Dacă aceasta ar fi restricția, grafurile plane ar necesita un număr arbitrar de mare de culori.
Alte false infirmări încalcă ipotezele teoremei în moduri neașteptate, cum ar fi utilizarea unei regiuni care are mai multe părți deconectate sau care nu permite ca regiunile de aceeași culoare să se atingă într-un punct.
Harta (stânga) a fost colorată cu cinci culori și este necesar să se modifice cel puțin patru din cele zece regiuni pentru a obține o colorare cu doar patru culori (dreapta).
Colorarea hărților politice
În viața reală, multe țări au exclave sau colonii. Deoarece acestea aparțin țării, trebuie să fie colorate cu aceeași culoare ca și țara-mamă. Aceasta înseamnă că, de obicei, sunt necesare mai mult de patru culori pentru a colora o astfel de hartă. Când matematicienii vorbesc despre graficul asociat problemei, ei spun că nu este planar. Chiar dacă este ușor de verificat dacă un grafic este planar, găsirea celui mai mic număr de culori necesare pentru a-l colora este foarte dificilă. Este NP-completă, ceea ce reprezintă una dintre cele mai dificile probleme care există. Cel mai mic număr de culori necesare pentru a colora un graf este cunoscut sub numele de număr cromatic al acestuia. Multe dintre problemele care apar atunci când se încearcă să se rezolve teorema celor patru culori sunt legate de matematica discretă. Din acest motiv, se folosesc adesea metode din topologia algebrică.
Extindere la hărțile "non-flat"
Teorema celor patru culori presupune ca "harta" să se afle pe o suprafață plană, ceea ce matematicienii numesc un plan. În 1890, Percy John Heawood a creat ceea ce astăzi se numește conjectura lui Heawood: Aceasta pune aceeași întrebare ca și teorema celor patru culori, dar pentru orice obiect topologic. De exemplu, un torus poate fi colorat cu cel mult șapte culori. Conjectura lui Heawood oferă o formulă care funcționează pentru toate aceste obiecte, cu excepția sticlei Klein.
Întrebări și răspunsuri
Î: Ce este teorema celor patru culori?
R: Teorema celor patru culori este o teoremă matematică care afirmă că în orice suprafață plană cu regiuni, regiunile pot fi colorate cu cel mult patru culori. Regiunile adiacente nu trebuie să primească aceeași culoare.
Î: Cum a fost stabilită prima demonstrație a teoremei celor patru culori?
R: Prima demonstrație a teoremei celor patru culori a fost o demonstrație prin epuizare cu 1.936 de cazuri. Aceasta înseamnă că a fost stabilită prin împărțirea în cazuri și demonstrarea fiecăruia separat.
Î: Sunt cartografii interesați de această problemă?
R: Nu, cartografii nu sunt foarte interesați de această problemă, deoarece hărțile care utilizează doar patru culori sunt rare și, de obicei, necesită doar trei culori. Cărțile de cartografie și de istorie a realizării hărților nu menționează proprietatea celor patru culori.
Î: Ce este teorema celor cinci culori?
R: Teorema celor cinci culori afirmă că cinci culori sunt suficiente pentru a colora o hartă și are o demonstrație scurtă și elementară care a fost demonstrată la sfârșitul secolului al XIX-lea.
Î: Cât de dificil a fost să se demonstreze că sunt necesare doar 4 culori pentru colorarea hărților?
R: Demonstrarea faptului că sunt necesare doar 4 culori pentru colorarea hărților s-a dovedit a fi mult mai dificilă decât se aștepta, deoarece au apărut multe dovezi false și contraexemple false de la prima sa afirmație din 1852.
Î: Există vreun exemplu de hartă în care ar fi necesare 5 sau mai multe culori pentru a colora corect toate regiunile?
R: Da, un astfel de exemplu este atunci când o regiune este înconjurată de un număr impar de alte regiuni care se ating între ele într-un ciclu - în acest caz, ar putea fi necesare 5 sau mai multe culori pentru a colora corect toate regiunile.
Căuta în

