Algebră | o parte a matematicii

Algebra (din arabă: الجبر, transliterat "al-jabr", care înseamnă "reunirea părților rupte") este o parte a matematicii. Ea utilizează variabile pentru a reprezenta o valoare care nu este încă cunoscută. Atunci când se folosește semnul egal (=), aceasta se numește ecuație. O ecuație foarte simplă care utilizează o variabilă este: 2 + 3 = x {\displaystyle 2+3=x} $2+3=x$ . În acest exemplu, x = 5 {\displaystyle x=5}. $x=5$ , sau se poate spune, de asemenea, că " x {\displaystyle x} este egal cu cinci". Acest lucru se numește rezolvare pentru x {\displaystyle x} .

Pe lângă ecuații, există și inegalități (mai mic decât și mai mare decât). Un tip special de ecuație se numește funcție. Aceasta este adesea utilizată la realizarea graficelor, deoarece transformă întotdeauna o intrare într-o ieșire.

Algebra poate fi folosită pentru a rezolva probleme reale, deoarece regulile algebrei funcționează în viața reală, iar numerele pot fi folosite pentru a reprezenta valorile unor lucruri reale. Fizica, ingineria și programarea calculatoarelor sunt domenii în care se folosește algebra în permanență. De asemenea, este util să o cunoști în topografie, construcții și afaceri, în special în contabilitate.

Persoanele care fac algebră folosesc regulile numerelor și operațiile matematice folosite pe numere. Cele mai simple sunt adunarea, scăderea, înmulțirea și împărțirea. Operațiile mai avansate implică exponenți, începând cu pătrate și rădăcini pătrate.

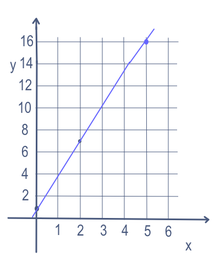
Algebra a fost folosită pentru prima dată pentru a rezolva ecuații și inegalități. Două exemple sunt ecuațiile liniare (ecuația unei linii drepte, y = m x + b {\displaystyle y=mx+b} $y=mx+b$ sau y = m x + c {\displaystyle y=mx+c} $y=mx+c$ ) și ecuațiile pătratice, care au variabilele care sunt ridicate la pătrat (înmulțite cu el însuși, de exemplu: 2 ⋅ 2 {\displaystyle 2\cdot 2} $2\cdot 2$ , 3 ⋅ 3 {\displaystyle 3\cdot 3} $3\cdot 3$ , sau x ⋅ x {\displaystyle x\cdot x} $x\cdot x$ ).

Istoric

Primele forme de algebră au fost dezvoltate de babilonieni și de geometri greci, cum ar fi Hero din Alexandria. Cu toate acestea, cuvântul "algebră" este o formă latină a cuvântului arab Al-Jabr ("turnare") și provine dintr-o carte de matematică Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Eseu despre calculul turnării și al ecuației") scrisă în secolul al IX-lea de un matematician persan, Muhammad ibn Mūsā al-Khwārizmī, care era un musulman născut în Khwarizm, în Uzbekistan. El a prosperat sub conducerea lui Al-Ma'moun în Bagdad, Irak, prin 813-833 d.Hr. și a murit în jurul anului 840 d.Hr. Cartea a fost adusă în Europa și tradusă în latină în secolul al XII-lea. Cartea a primit apoi numele de "Algebră". (Finalul numelui matematicianului, al-Khwarizmi, a fost schimbat într-un cuvânt mai ușor de pronunțat în latină și a devenit cuvântul englezesc "algoritm").

Exemple

Iată un exemplu simplu de problemă de algebră:

Sue are 12 bomboane, iar Ann are 24 de bomboane. Ele decid să împartă astfel încât să aibă același număr de bomboane. Câte bomboane va avea fiecare?

Aceștia sunt pașii pe care îi puteți utiliza pentru a rezolva problema:

Pentru a avea același număr de bomboane, Ann trebuie să îi dea câteva lui Sue. Fie ca x {\displaystyle x} să reprezinte numărul de bomboane pe care Ann i le dă lui Sue.
Bomboanele lui Sue, plus x {\displaystyle x} , trebuie să fie la fel ca bomboanele lui Ann minus x {\displaystyle x} . Acest lucru se scrie ca: 12 + x = 24 - x {\displaystyle 12+x=24-x}. $12+x=24-x$
Scădeți 12 din ambele părți ale ecuației. Rezultă: x = 12 - x {\displaystyle x=12-x} $x=12-x$ . (Ceea ce se întâmplă de o parte a semnului egal trebuie să se întâmple și de cealaltă parte, pentru ca ecuația să fie în continuare adevărată. Deci, în acest caz, atunci când 12 a fost scăzut din ambele părți, a existat un pas intermediar de 12 + x - 12 = 24 - x - 12 {\displaystyle 12+x-12=24-x-12} $12+x-12=24-x-12$ . După ce o persoană se simte confortabil cu acest lucru, pasul din mijloc nu se mai scrie).
Adăugați x {\displaystyle x} la ambele părți ale ecuației. Rezultă: 2 x = 12 {\displaystyle 2x=12}. $2x=12$
Împărțiți ambele părți ale ecuației la 2. Rezultă x = 6 {\displaystyle x=6} $x=6$ . Răspunsul este 6. Aceasta înseamnă că dacă Ann îi dă lui Sue 6 bomboane, vor avea același număr de bomboane.
Pentru a verifica acest lucru, puneți 6 înapoi în ecuația originală, oriunde x {\displaystyle x} a fost: 12 + 6 = 24 - 6 {\displaystyle 12+6=24-6}. $12+6=24-6$
Acest lucru dă 18 = 18 {\displaystyle 18=18} $18=18$ , ceea ce este adevărat. Fiecare dintre ei are acum 18 bomboane.

Cu ajutorul practicii, algebra poate fi folosită atunci când se confruntă cu o problemă care este prea greu de rezolvat în alt mod. Probleme precum construcția unei autostrăzi, proiectarea unui telefon mobil sau găsirea leacului pentru o boală, toate necesită algebră.

Scrierea algebrei

La fel ca în cele mai multe părți ale matematicii, adăugarea lui y {\displaystyle y} la z {\displaystyle z} $z$ (sau y {\displaystyle y} plus z {\displaystyle z} $z$ ) se scrie y + z {\displaystyle y+z} $y+z$ ;

scăzând z {\displaystyle z} $z$ din y {\displaystyle y} (sau y {\displaystyle y} minus z {\displaystyle z} $z$ ) se scrie ca y - z {\displaystyle y-z} $y-z$ ;

iar împărțirea lui y {\displaystyle y} la z {\displaystyle z} $z$ (sau y {\displaystyle y} la z {\displaystyle z} $z$ ) se scrie ca y / z {\displaystyle y/z} $y/z$ sau y z {\displaystyle y \ over z} ${y \over z}$ .

În algebră, înmulțirea lui y {\displaystyle y} cu z {\displaystyle z} $z$ (sau y {\displaystyle y} înmulțit cu z {\displaystyle z} $z$ ) poate fi scrisă în 3 moduri diferite: y ⋅ z {\displaystyle y\cdot z} $y\cdot z$ , y ( z ) {\displaystyle y(z)} $y(z)$ sau pur și simplu y z {\displaystyle yz} $yz$ . Toate aceste notații înseamnă același lucru: y {\displaystyle y} ori z {\displaystyle z} $z$ . Simbolul " × { {\displaystyle \times } $\times$ " utilizat în aritmetică nu este folosit în algebră, deoarece seamănă prea mult cu litera x {\displaystyle x} , care este adesea folosită ca variabilă.

Când înmulțim un număr și o variabilă în algebră, putem scrie pur și simplu numărul în fața literei: 5 ⋅ y ⟺ 5 y {\displaystyle 5\cdot y\iff 5y} $5\cdot y\iff 5y$ . Când numărul este 1, atunci nu se scrie, deoarece 1 ori orice număr este acel număr ( 1 ⋅ y = y {\displaystyle 1\cdot y=y} $1\cdot y=y$ ) și deci nu este necesar. Iar atunci când este 0, putem elimina complet termenii, deoarece 0 ori orice număr este zero ( 0 ⋅ y = 0 {\displaystyle 0\cdot y=0} $0\cdot y=0$ ).

Ca o notă suplimentară, nu trebuie să folosiți literele x {\displaystyle x} sau y {\displaystyle y} în algebră. Variabilele sunt doar simboluri care semnifică un număr sau o valoare necunoscută, așa că puteți folosi orice literă pentru o variabilă (cu excepția lui e {\displaystyle e} $e$ (numărul lui Euler) și i {\displaystyle i} $i$ (unitate imaginară), deoarece acestea sunt constante matematice). x {\displaystyle x} și y {\displaystyle y} sunt cele mai comune, totuși.

Funcții și grafice

O parte importantă a algebrei este studiul funcțiilor, deoarece acestea apar adesea în ecuațiile pe care încercăm să le rezolvăm. O funcție este ca o mașinărie în care se poate introduce un număr (sau mai multe numere) și din care se poate obține un anumit număr (sau mai multe numere). Atunci când folosim funcții, graficele pot fi instrumente puternice pentru a ne ajuta să studiem soluțiile ecuațiilor.

Un grafic este o imagine care arată toate valorile variabilelor care fac ca ecuația sau inegalitatea să fie adevărată. De obicei, acest lucru este ușor de realizat atunci când există doar una sau două variabile. Graficul este adesea o linie, iar dacă linia nu se îndoaie sau nu merge drept în sus și în jos, poate fi descrisă prin formula de bază y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Variabila b {\displaystyle b} $b$ reprezintă interceptarea y a graficului (punctul în care linia intersectează axa verticală), iar m {\displaystyle m} reprezintă panta sau abruptul liniei. Această formulă se aplică coordonatelor unui grafic, unde fiecare punct de pe dreaptă se scrie ( x {\displaystyle x} , y {\displaystyle y} ).

În unele probleme de matematică, cum ar fi ecuația unei linii, pot exista mai multe variabile ( x {\displaystyle x} și y {\displaystyle y} în acest caz). Pentru a găsi punctele de pe dreaptă, se schimbă o variabilă. Variabila care se modifică se numește variabilă "independentă". Apoi se face calculele matematice pentru a obține un număr. Numărul obținut se numește variabila "dependentă". De cele mai multe ori, variabila independentă este scrisă ca x {\displaystyle x} , iar variabila dependentă este scrisă ca y {\displaystyle y}. , de exemplu, în y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$ . Acest lucru este adesea pus pe un grafic, folosind o axă x {\displaystyle x} (care merge spre stânga și spre dreapta) și o axă y {\displaystyle y} (care merge în sus și în jos). De asemenea, poate fi scris sub formă de funcție: f ( x ) = 3 x + 1 {\displaystyle f(x)=3x+1} $f(x)=3x+1$ . Deci, în acest exemplu, am putea introduce 5 pentru x {\displaystyle x} și să obținem y = 16 {\displaystyle y=16}. $y=16$ . Dacă am introduce 2 pentru x {\displaystyle x} am obține y = 7 {\displaystyle y=7} $y=7$ . Și 0 pentru x {\displaystyle x} ar obține y = 1 {\displaystyle y=1} $y=1$ . Deci ar exista o dreaptă care trece prin punctele (5,16), (2,7) și (0,1), așa cum se vede în graficul din dreapta.

Dacă x {\displaystyle x} are o putere de 1, este o linie dreaptă. Dacă este la pătrat sau la o altă putere, va fi curbă. Dacă se folosește o inegalitate ( < {\displaystyle <} $<$ sau > {\displaystyle >} $>$ ), atunci, de obicei, o parte a graficului este umbrită, fie deasupra, fie sub linie.

Ecuație liniară pentru y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$

Reguli

În algebră, există câteva reguli care pot fi folosite pentru o mai bună înțelegere a ecuațiilor. Acestea se numesc reguli de algebră. Deși aceste reguli pot părea fără sens sau evidente, este înțelept să înțelegem că aceste proprietăți nu sunt valabile în toate ramurile matematicii. Prin urmare, va fi util să cunoaștem cum sunt declarate aceste reguli axiomatice, înainte de a le lua ca fiind de la sine înțelese. Înainte de a trece la reguli, reflectați asupra a două definiții care vor fi date.

Opusul: opusul unui {\displaystyle a} este - un {\displaystyle -a} .
Reciprocă: reciproca unui {\displaystyle a} este 1 a {\displaystyle {\frac {1}{a}}}} ${\frac {1}{a}}$ .

Proprietatea comutativă a adunării

"Comutativă" înseamnă că o funcție are același rezultat dacă numerele sunt schimbate. Cu alte cuvinte, ordinea termenilor dintr-o ecuație nu contează. Atunci când se adaugă doi termeni (adunări), se aplică "proprietatea comutativă a adunării". În termeni algebrici, rezultă a + b = b + a {\displaystyle a+b=b+a} a+b=b+a .

Rețineți că acest lucru nu se aplică în cazul scăderii (adică a - b ≠ b - a {\displaystyle a-b\neq b-a} $a-b\neq b-a$ cu excepția cazului în care a = b {\displaystyle a=b} $a=b$ ).

Proprietatea comutativă a înmulțirii

Atunci când se înmulțesc doi termeni (factori), se aplică "proprietatea comutativă a înmulțirii". În termeni algebrici, rezultă a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} $a\cdot b=b\cdot a$ .

Rețineți că acest lucru nu se aplică în cazul diviziunii (de exemplu, a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}}. ${\frac {a}{b}}\neq {\frac {b}{a}}$ , când a ≠ 0 {\displaystyle a\neq 0} $a\neq 0$ și b ≠ 0 {\displaystyle b\neq 0} $b\neq 0$ , cu excepția cazului în care a = b {\displaystyle a=b} $a=b$ ).

Proprietatea asociativă a adunării

"Asociativ" se referă la gruparea numerelor. Proprietatea asociativă a adunării implică faptul că, atunci când se adună trei sau mai mulți termeni, nu contează cum sunt grupați acești termeni. Din punct de vedere algebric, rezultă a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Rețineți că acest lucru nu este valabil pentru scădere, de exemplu, 1 - ( 2 - 3 ) ≠ ( 1 - 2 ) - 3 {\displaystyle 1-(2-3)\neq (1-2)-3} $1-(2-3)\neq (1-2)-3$ (a se vedea proprietatea distributivă).

Proprietatea asociativă a înmulțirii

Proprietatea asociativă a înmulțirii implică faptul că, atunci când se înmulțesc trei sau mai mulți termeni, nu contează cum sunt grupați acești termeni. Din punct de vedere algebric, rezultă a ( b c ) = ( a b ) c {\displaystyle a(bc)=(ab)c} $a(bc)=(ab)c$ . Rețineți că acest lucru nu este valabil pentru diviziune, de exemplu 1 / ( 2 / 4 ) ≠ ( 1 / 2 ) / 4 {\displaystyle 1/(2/4)\neq (1/2)/4} $1/(2/4)\neq (1/2)/4$ .

Proprietatea distributivă

Proprietatea distributivă afirmă că înmulțirea unui termen cu un alt termen poate fi distribuită. De exemplu: a ( b + c ) = a b + a c {\displaystyle a(b+c)=ab+ac} $a(b+c)=ab+ac$ . (Nu confundați acest lucru cu proprietățile asociative! De exemplu: a ( b + c ) ≠ ( a b ) + c {\displaystyle a(b+c)\neq (ab)+c} $a(b+c)\neq (ab)+c$ .) .)

Identitate aditivă

"Identitatea" se referă la proprietatea unui număr de a fi egal cu el însuși. Cu alte cuvinte, există o operație de adunare a două numere astfel încât acesta să fie egal cu variabila sumei. Proprietatea de identitate aditivă afirmă că orice număr plus 0 este acel număr: a + 0 = a {\displaystyle a+0=a} a+0=a . Acest lucru este valabil și pentru scădere: a - 0 = a {\displaystyle a-0=a} a-0=a .

Identitate multiplicativă

Proprietatea identității multiplicative afirmă că orice număr înmulțit cu 1 este acel număr: a ⋅ 1 = a {\displaystyle a\cdot 1=a} $a\cdot 1=a$ . Acest lucru este valabil și pentru împărțire: a 1 = a {\displaystyle {\frac {a}{1}}}=a} ${\frac {a}{1}}=a$ .

Proprietatea aditivă inversă

Proprietatea inversă aditivă este oarecum opusul identității aditive. Atunci când adunăm un număr și opusul său, rezultatul este 0. Algebric, aceasta afirmă următoarele: a + - a = 0 {\displaystyle a+-a=0}. $a+-a=0$ , ceea ce este același lucru cu a - a = 0 {\displaystyle a-a=0} $a-a=0$ . De exemplu, inversul aditiv (sau opusul) lui 1 este -1.

Proprietatea inversă multiplicativă

Proprietatea inversă multiplicativă înseamnă că, atunci când înmulțim un număr și inversul său, rezultatul este 1. Algebric, aceasta afirmă următoarele: a ⋅ $a\cdot {\frac {1}{a}}=1$ , ceea ce este același lucru cu a a = 1 {\displaystyle {\frac {a}{a}}=1} ${\frac {a}{a}}=1$ . De exemplu, inversa multiplicativă (sau doar inversa) a lui 2 este 1/2. Pentru a obține inversa unei fracții, schimbați numărătorul și numitorul: inversa lui 2 3 {\displaystyle {\frac {2}{3}}} ${\frac {2}{3}}$ este 3 2 {\displaystyle {\frac {\frac {3}{2}}} ${\frac {3}{2}}$ .

Algebră avansată

Pe lângă "algebra elementară", sau algebra de bază, există forme avansate de algebră, predate în colegii și universități, cum ar fi algebra abstractă, algebra liniară și algebra universală. Aceasta include modul de utilizare a unei matrice pentru a rezolva mai multe ecuații liniare deodată. Algebra abstractă este studiul lucrurilor care se regăsesc în ecuații, trecând dincolo de numere și ajungând la mai mult abstract cu grupuri de numere.

Multe probleme de matematică se referă la fizică și inginerie. În multe dintre aceste probleme de fizică, timpul este o variabilă. Litera folosită pentru timp este t {\displaystyle t} $t$ . Utilizarea ideilor de bază din algebră poate ajuta la reducerea unei probleme de matematică la forma sa cea mai simplă, facilitând astfel rezolvarea problemelor dificile. Energia este e {\displaystyle e}. $e$ , forța este f {\displaystyle f} , masa este m {\displaystyle m} . , accelerația este a {\displaystyle a} și viteza luminii este uneori c {\displaystyle c} $c$ . Acest lucru este utilizat în unele ecuații celebre, cum ar fi f = m a {\displaystyle f=ma} $f=ma$ și e = m c 2 {\displaystyle e=mc^{2}}. $e=mc^{2}$ (deși a fost nevoie de o matematică mai complexă, dincolo de algebră, pentru a ajunge la această ultimă ecuație).

Pagini conexe

Lista de subiecte de matematică
Ordinea operațiunilor
Parabola
Sistem de algebră pe calculator

Întrebări și răspunsuri

Î: Ce este algebra?

R: Algebra este o parte a matematicii care utilizează variabile pentru a reprezenta o valoare care nu este încă cunoscută.

Î: Ce înseamnă semnul egal în algebră?

R: Semnul egal (=) semnifică o ecuație în algebră.

Î: Ce este o funcție în algebră?

R: O funcție în algebră este un tip special de ecuație care transformă întotdeauna o intrare într-o ieșire.

Î: Cum poate fi utilizată algebra pentru a rezolva probleme reale?

R: Algebra poate fi utilizată pentru a rezolva probleme reale deoarece regulile algebrei funcționează în viața reală, iar numerele pot fi utilizate pentru a reprezenta valorile unor lucruri reale. Fizica, ingineria și programarea calculatoarelor sunt domenii în care se folosește algebra tot timpul. De asemenea, este util să o cunoașteți în topografie, construcții și afaceri, în special în contabilitate.

Î: Care sunt unele operații matematice utilizate pe numere în algebră?

R: În algebră, oamenii folosesc regulile numerelor și operațiile matematice, cum ar fi adunarea, scăderea, înmulțirea și împărțirea numerelor. Operațiile mai avansate implică exponenți, începând cu pătrate și rădăcini pătrate.

Î: Care sunt exemple de ecuații utilizate în algebră?

R: Printre exemplele de ecuații utilizate în algebră se numără ecuațiile liniare (ecuația unei linii drepte) și ecuațiile pătratice care au variabile care sunt ridicate la pătrat (înmulțite cu sine).