Algoritm

Compararea algoritmilor

De obicei, există mai multe moduri de a rezolva o problemă. Pot exista mai multe rețete diferite pentru a face un anumit fel de mâncare care arată diferit, dar care, la final, are același gust. Același lucru este valabil și în cazul algoritmilor. Cu toate acestea, unele dintre aceste modalități vor fi mai bune decât altele. Dacă o rețetă are nevoie de o mulțime de ingrediente complicate pe care nu le aveți, aceasta nu este la fel de bună ca o rețetă simplă. Atunci când analizăm algoritmii ca modalitate de rezolvare a problemelor, deseori dorim să știm cât timp i-ar lua unui computer să rezolve problema folosind un anumit algoritm. Atunci când scriem algoritmi, ne dorim ca algoritmul nostru să dureze cât mai puțin timp, astfel încât să putem rezolva problema cât mai repede posibil.

În bucătărie, unele rețete sunt mai greu de făcut decât altele, pentru că necesită mai mult timp pentru a fi terminate sau pentru că trebuie să țineți cont de mai multe lucruri. Același lucru este valabil și pentru algoritmi, iar algoritmii sunt mai buni atunci când sunt mai ușor de realizat de către computer. Lucrul care măsoară dificultatea unui algoritm se numește complexitate. Atunci când întrebăm cât de complex este un algoritm, deseori vrem să știm cât timp îi va lua unui computer să rezolve problema pe care dorim să o rezolve.

Sortare

Acesta este un exemplu de algoritm de sortare a cărților cu culori în grămezi de aceeași culoare:

1. Ridicați toate cărțile.
2. Alegeți o carte din mână și priviți culoarea cărții.
3. Dacă există deja o grămadă de cărți de acea culoare, puneți această carte pe acea grămadă.
4. Dacă nu există nicio grămadă de cărți de acea culoare, faceți o nouă grămadă doar din această culoare.
5. Dacă mai aveți încă o carte în mână, reveniți la pasul al doilea.
6. Dacă nu mai aveți nicio carte în mână, atunci cărțile sunt sortate. Ați terminat.

Sortarea după numere

Acestea sunt exemple de algoritmi de sortare a unui teanc de cărți cu mai multe numere diferite, astfel încât numerele să fie în ordine.

Jucătorii încep cu un teanc de cărți care nu au fost sortate.

Primul algoritm

Acest algoritm trece prin stiva de cărți, câte o carte pe rând. Această carte este comparată cu următoarea carte din stivă. Vă rugăm să rețineți că această poziție se schimbă doar în etapa 6. Acest algoritm se numește "bubble sort". Este lent.

1. Dacă teancul de cărți este gol sau conține doar o singură carte, acesta este sortat; ați terminat.
2. Luați teancul de cărți. Uitați-vă la prima carte (cea de sus) din teanc.
3. Cartea pe care o priviți este cartea A. Poziția în care se află cartea A este în stiva P.
4. Dacă nu mai există alte cărți în stivă după cartea A, treceți la pasul 8.
5. Următoarea carte din teanc este cartea B.
6. Dacă cartea B are un număr mai mic decât cartea A, schimbați pozițiile cărților A și B. Amintiți-vă că ați făcut acest lucru. Când schimbați cărțile, nu schimbați poziția P.
7. Dacă există o altă carte în stivă după poziția P, uitați-vă la ea; reveniți la pasul 3.
8. Dacă nu ați schimbat poziția niciunei cărți în ultima rundă, ați terminat; teancul de cărți este sortat.
9. În caz contrar, reveniți la pasul 2.

Exemplu pas cu pas

Să luăm un teanc de cărți cu numerele "5 1 4 2 8" și să le sortăm de la cel mai mic număr la cel mai mare folosind acest algoritm. În fiecare pas, algoritmul compară elementele scrise cu bold. Partea de sus a teancului de cărți se află în partea stângă.

Prima trecere:
( 5 1 4 2 8 ) → {\displaystyle \to } ( 1 5 5 4 2 8 ) Aici, algoritmul compară primele două elemente și le schimbă.
( 1 5 5 4 2 8 ) → {\displaystyle \to }
( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 2 5 8 )
( 1 4
2 5 8 ) → {\displaystyle \to } ( 1 4 2 2 5 8 ) Aceste elemente sunt deja în ordine, astfel încât algoritmul nu le schimbă.
A doua trecere:
( 1 4 2 5 8 ) → {\displaystyle \to } (
1 4 2 5 8 ) (
1 4 2 5 8 ) → {\displaystyle \to } (
1 2 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } (
1 2 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 2 4 5 8 )
Acum, teancul de cărți este deja sortat, dar algoritmul nostru nu știe acest lucru. Algoritmul are nevoie de o singură trecere fără niciun schimb pentru a ști că este sortat.
A treia trecere:
( 1 2 4 5 8 ) → {\displaystyle \to } (
1 2 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } (
1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } (
1 2 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 5 8 )În cele
din urmă, matricea este sortată, iar algoritmul se poate opri.

Istorie

Acesta este un algoritm de sortare ușor de înțeles. Informaticienii l-au numit Bubble sort (sortare cu bule), deoarece elementele mai mici vor urca în vârf, schimbându-și poziția la fiecare rulare. Din păcate, algoritmul nu este foarte bun, deoarece are nevoie de mult timp (multe treceri prin stiva de cărți) pentru a o sorta.

Al doilea algoritm

Acest algoritm folosește o altă idee. Uneori, rezolvarea unei probleme este dificilă, dar problema poate fi schimbată astfel încât să fie formată din probleme mai simple și mai ușor de rezolvat. Acest lucru se numește recursivitate. Este mai dificil de înțeles decât primul exemplu, dar va oferi un algoritm mai bun.

Ideea de bază

1. Dacă stiva nu are nicio carte sau are doar o singură carte, este sortată și ați terminat.
2. Împărțiți teancul de cărți în două jumătăți de aproximativ aceeași mărime. Dacă există un număr impar de cărți, unul dintre cele două teancuri va avea o carte în plus față de celălalt.
3. Sortați fiecare dintre cele două stive folosind acest algoritm (Pentru fiecare stivă, începeți de la elementul 1 din această listă.)
4. Îmbinați cele două stive sortate, așa cum este descris mai jos.
5. Rezultatul este un teanc de cărți sortate. Ați terminat.

Unirea a două stive

Acest lucru funcționează cu două teancuri de cărți. Una dintre ele se numește A, iar cealaltă se numește B. Există o a treia stivă, numită C, care este goală la început și care va conține rezultatul.

1. Dacă fie stiva A, fie stiva B este goală, puneți toate cărțile din stiva care nu este goală deasupra stivei C; ați terminat, stiva C este rezultatul fuziunii. (Notă: luați tot teancul și puneți-l pe teancul C; dacă o faceți carte cu carte, veți schimba ordinea și nu va funcționa așa cum ar trebui).
2. Uitați-vă la cărțile de sus din teancul A și din teancul B. Puneți-o pe cea cu numărul cel mai mic deasupra teancul C. Dacă teancul C nu conținea nicio carte, acum va avea o carte.
3. Dacă din stiva A sau din stiva B au rămas cărți, reveniți la pasul 1 pentru a le sorta.

Istorie

John von Neumann a dezvoltat acest algoritm în 1945. El nu l-a numit Sortare după numere, ci Mergesort. Este un algoritm foarte bun de sortare, în comparație cu alții.

Al treilea algoritm

Primul algoritm are nevoie de mult mai mult timp pentru a sorta cărțile decât al doilea, dar poate fi îmbunătățit. Dacă ne uităm la sortarea cu bule, se poate observa că cărțile cu numere mari se mută din partea de sus a stivei destul de repede, dar cărților cu numere mici de la baza stivei le ia mult timp să urce (să se mute în partea de sus). Pentru a îmbunătăți primul algoritm, iată care este ideea:

În loc să se compare două cărți care se află una lângă cealaltă, la început se alege o carte "specială". Toate celelalte cărți sunt apoi comparate cu această carte.

1. Începem cu o stivă A. Vor exista alte două stive B și C, care vor fi create ulterior.
2. Dacă stiva A nu are nicio carte sau are doar o singură carte, am terminat sortarea.
3. Se alege o carte din stiva A, dacă este posibil la întâmplare. Aceasta se numește pivot.
4. Toate cărțile rămase din teancul A sunt comparate cu acest pivot. Cărțile cu un număr mai mic merg în stiva B, iar cele cu un număr egal sau mai mare merg în stiva C.
5. Dacă există cărți în teancurile B sau C, aceste teancuri trebuie sortate cu același algoritm (începeți de la poziția 1 din această listă atât pentru teancul B, cât și pentru teancul C, pe rând).
6. S-a făcut. Stiva de cărți sortate are mai întâi stiva B, apoi pivotul și apoi stiva C.

Istorie

Acest algoritm a fost dezvoltat de C. A. R. Hoare în 1960. Este unul dintre cei mai utilizați algoritmi de sortare din prezent. Se numește Quicksort.

Animație care arată cum funcționează o sortare cu bule


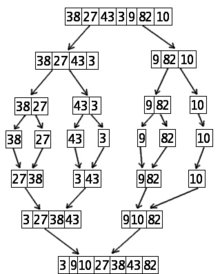
Sortarea a 7 numere utilizând al doilea algoritm de sortare după numere (Mergesort)


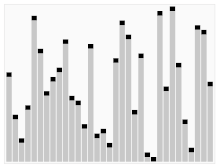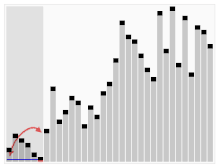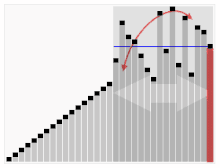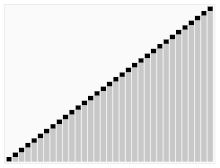
Al treilea algoritm de sortare a cărților. Elementul cu bara roșie este ales ca pivot. La început, acesta este elementul care se află tot la dreapta. Acest algoritm se numește Quicksort.

Punerea laolaltă a algoritmilor

Dacă jucătorii au cărți cu culori și numere pe ele, le pot sorta după culori și numere dacă aplică algoritmul "sortare după culori", apoi aplică algoritmul "sortare după numere" la fiecare teanc de cărți colorate, apoi pun teancurile împreună.

Algoritmii de sortare după numere sunt mai dificil de realizat decât algoritmul de sortare după culori, deoarece este posibil să fie nevoie să repete pașii de mai multe ori. S-ar putea spune că sortarea după numere este mai complexă.

Pagini conexe

• Algoritmul euclidian a fost descoperit în urmă cu peste 2000 de ani. Acesta este capabil să găsească cel mai mare divizor comun a două numere.