Algebră elementară
Algebra elementară este cea mai elementară formă de algebră predată elevilor. Este adesea unul dintre următoarele domenii ale matematicii predate elevilor, după aritmetică. În timp ce în aritmetică apar doar numere și operatori precum +, -, × și ÷, în algebră, variabilele (precum a, x, y) sunt folosite pentru a reprezenta numere. Acest lucru este util deoarece:
- Acesta permite oamenilor să rezolve probleme legate de numere "necunoscute". Acest lucru înseamnă să înveți despre ecuații și cum să le rezolvi (de exemplu, "găsiți un număr x în care 3 x + 1 = 10 {\displaystyle 3x+1=10}
").
- Aceasta permite generalizarea regulilor din aritmetică. În timp ce unii elevi înțeleg că 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}
, este util să demonstreze că a + b = b + a {\displaystyle a+b=b+a}
pentru toate a și b. Acest lucru face ca algebra să fie un pas bun pentru a învăța despre abstractizare (învățarea ideilor generale din mai multe exemple).
- Ajută oamenii să înțeleagă și să creeze relații funcționale (uneori numite și relații de cauză și efect). Un exemplu este "dacă se vând x bilete, profitul va fi de 3 x - 10 {\displaystyle 3x-10}
dolari".
Acestea trei sunt principalele componente ale algebrei elementare. Algebra elementară este adesea utilizată în multe alte materii, cum ar fi științele, afacerile și construcțiile. Algebra abstractă, un subiect mult mai avansat, este în general predată târziu în facultate.
Probleme simple de algebră
Dacă o ecuație are un singur număr necunoscut, este uneori ușor de rezolvat. Numărul necunoscut se numește "x":
2 x + 4 = 12. {\displaystyle 2x+4=12.\,}
Pentru a rezolva o ecuație simplă cu o singură necunoscută, adăugați, scădeți, înmulțițiți sau împărțiți ambele părți ale ecuației cu același număr pentru a plasa necunoscuta, x, pe o parte a ecuației. Odată ce x se află de unul singur pe o parte, utilizați aritmetica pentru a determina suma de pe cealaltă parte a ecuației. De exemplu, scăzând 4 din ambele părți ale ecuației de mai sus:
2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4-4=12-4\,}
obținerea:
2 x = 8 {\displaystyle 2x=8\,}
Împărțind ambele părți cu 2:
2 x 2 2 = 8 2 {\displaystyle {\frac {2x}{2}}}={\frac {8}{2}}}\,}
obținerea:
x = 4. {\displaystyle x=4.\,}
Poate fi de ajutor să vă gândiți la această ecuație ca la un balansoar sau o balanță: ceea ce faceți pe o parte, trebuie să faceți pe cealaltă, iar scopul principal este să obțineți x de la sine.
Definiții
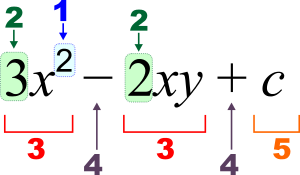
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c}
1 : Exponent (putere), 2 : Coeficient, 3 : termen, 4 : operator, 5 : constantă, x , y {\displaystyle x,y} : 
Întrebări și răspunsuri
Î: Ce este algebra elementară?
R: Algebra elementară este cea mai elementară formă de algebră predată elevilor. De obicei, urmează aritmetica și implică utilizarea variabilelor (cum ar fi a, x, y) pentru a reprezenta numere în ecuații.
Î: Care sunt unele utilizări ale algebrei elementare?
R: Algebra elementară poate fi utilizată pentru a rezolva probleme legate de numere necunoscute, pentru a generaliza reguli din aritmetică, pentru a înțelege și a crea relații funcționale și este adesea utilizată în multe alte materii, cum ar fi științele, afacerile și construcțiile.
Î: Cum îi ajută algebra elementară pe oameni să înțeleagă ideile abstracte?
R: Algebra elementară îi ajută pe oameni să învețe idei generale pornind de la multe exemple, demonstrând că a+b=b+a pentru toate a și b. Acest lucru le permite să înțeleagă mai bine conceptele abstracte.
Î: Este algebra abstractă mai avansată decât algebra elementară?
R: Da, algebra abstractă este, în general, predată târziu în facultate și este mult mai avansată decât algebra elementară.
Î: Ce tipuri de ecuații implică algebra elementară?
R: Algebra elementară implică ecuații cu variabile (cum ar fi a, x, y) care reprezintă numere, precum și operatori precum +,- ,× ,și ÷ .
3x+1=10 {\displaystyle 3x+1=10}
Î: Cum poate ajuta înțelegerea algebrei elementare la alte materii?
R: Înțelegerea algebrei elementare poate fi utilă în cadrul altor materii, cum ar fi științele, afacerile sau construcțiile, deoarece permite oamenilor să rezolve probleme legate de numere necunoscute și să creeze relații funcționale între diferite variabile.
Căuta în




