Fractal

Exemple

Există multe tipuri de fractale, realizate într-o mare varietate de moduri. Un exemplu este triunghiul Sierpinski, în care există un număr infinit de triunghiuri mici în interiorul celui mare. Un alt exemplu este setul Mandelbrot, numit după Benoît Mandelbrot. Triunghiul Sierpinksi este construit cu ajutorul unor modele, dar setul Mandelbrot se bazează pe o ecuație.

Există, de asemenea, multe exemple naturale de fractali în natură, inclusiv copaci, fulgi de zăpadă, unele legume și linii de coastă.

Curba lui Koch

Curba lui Koch este un exemplu simplu de fractal. În primul rând, începeți cu o parte a unei linii drepte - numită segment de dreaptă. Tăiați linia în 3 bucăți de aceeași mărime. Scăpați de mijlocul acestor bucăți și puneți în partea de sus a unui triunghi cu laturile care au aceeași lungime ca și bucățica de tăiat. Avem acum 4 segmente de dreaptă care se ating la capete. Acum putem face ceea ce tocmai am făcut cu primul segment pentru fiecare dintre cele 4 bucăți. Acum putem face același lucru din nou și din nou pentru toate bucățile pe care le avem. Facem acest lucru la nesfârșit și ne uităm la ce obținem.

Lungimea curbei Koch este infinită, iar aria curbei Koch este zero. Acest lucru este destul de ciudat. Un segment de dreaptă (cu dimensiunea 1) ar putea avea lungimea 1, dar are aria 0. Un pătrat de lungime 1 și lățime 1 (cu dimensiunea 2) va avea aria 1 și lungimea infinită.

Dimensiunea de similitudine

Astfel, curba lui Koch pare să fie mai mare decât ceva de dimensiunea 1 și mai mică decât ceva de dimensiunea 2. Ideea dimensiunii de similaritate este de a oferi o dimensiune care să ofere o idee mai bună despre lungime sau suprafață pentru fractali. Așadar, pentru o curbă Koch, dorim o dimensiune între 1 și 2.

Curba lui Koch poate fi tăiată în patru bucăți, fiecare dintre ele având 1 3 {\displaystyle {\frac {1}{3}}} din dimensiunea originalului. Numim numărul de bucăți în care poate fi tăiat un fractal N {\displaystyle N} , iar diferența de mărime B {\displaystyle B} . Introducem aceste valori în ecuație:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}}}

Unde log {\displaystyle \log } este logaritmul unui număr. Acest număr este dimensiunea Hausdorff a fractalului. În cazul curbei Koch, aceasta este log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619... } așa cum am dorit.

Curba Koch este una dintre cele mai simple forme fractale, astfel încât dimensiunea sa este ușor de calculat. Dimensiunea de similaritate și dimensiunea Hausdorff sunt ambele identice. Acest lucru nu este valabil pentru fractalele mai complexe.

Fulg de nea Koch

Fulgul de zăpadă Koch (sau steaua Koch) este la fel ca și curba Koch, cu excepția faptului că începe cu un triunghi echilateral în loc de un segment de dreaptă.

Cum se realizează curba Koch

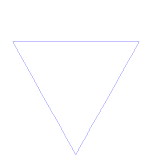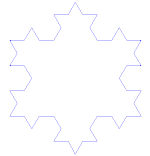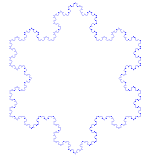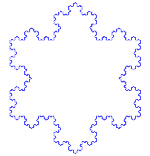
Utilizează

Fractalii au numeroase aplicații, de exemplu în biologie (plămâni, rinichi, variabilitatea ritmului cardiac etc.), în cutremure, în finanțe, unde sunt legați de așa-numitele distribuții cu coadă grea și în fizică. Acest lucru indică faptul că fractalii ar trebui să fie studiați pentru a înțelege de ce sunt atât de frecvenți în natură.

Unele fractale există doar din motive artistice, dar altele sunt foarte utile. Fractalii sunt forme foarte eficiente pentru antenele radio și sunt folosiți în cipurile de calculator pentru a conecta eficient toate componentele. De asemenea, liniile de coastă pot fi privite ca fractale.