Dimensiune | matematică și fizică
Dimensiunile reprezintă modul în care vedem, măsurăm și experimentăm lumea noastră, prin utilizarea dimensiunilor de sus în jos, de la dreapta la stânga, de la spate în față, de la cald la rece, cât de greu și cât de lung, precum și a unor concepte mai avansate din matematică și fizică. Un mod de a defini o dimensiune este să ne uităm la gradele de libertate sau la modul în care un obiect se poate mișca într-un anumit spațiu. Există diferite concepte sau moduri în care este folosit termenul de dimensiune și există, de asemenea, diferite definiții. Nu există o definiție care să satisfacă toate conceptele.
Într-un spațiu vectorial 
(în care vectorii sunt "săgeți" cu direcții), dimensiunea lui V , scrisă, de asemenea, ca 
, este egală cu cardinalitatea (sau numărul de vectori) unei baze a lui (un set care indică câte direcții unice are de fapt ). Este, de asemenea, egală cu numărul celui mai mare grup de direcții de linii drepte din spațiul respectiv. Obiectele "normale" din viața de zi cu zi sunt specificate de trei dimensiuni, care se numesc de obicei lungime, lățime și adâncime. Matematicienii numesc acest concept spațiu euclidian.
Dimensiunile pot fi utilizate și pentru a măsura poziția. Distanța până la o poziție de la un punct de plecare poate fi măsurată în direcția lungimii, lățimii și înălțimii. Aceste distanțe reprezintă o măsură a poziției.
În unele ocazii, o a patra dimensiune (4D), timpul, este folosită pentru a arăta poziția unui eveniment în timp și spațiu.
O diagramă a primelor patru dimensiuni spațiale.
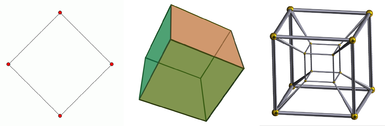
De la stânga la dreapta, pătratul, cubul și teseracul. Pătratul este un obiect bidimensional, cubul este un obiect tridimensional, iar teseractul este un obiect cvadridimensional. Un obiect unidimensional este doar o linie. Se oferă o proiecție a cubului, deoarece acesta este vizualizat pe un ecran bidimensional. Același lucru este valabil și pentru tesseract, care, în plus, nu poate fi prezentat decât ca o proiecție, chiar și în spațiul tridimensional.
Alte dimensiuni
În știința modernă, oamenii folosesc alte dimensiuni. Dimensiuni precum temperatura și greutatea pot fi folosite pentru a arăta poziția unui lucru în spații mai puțin simple. Oamenii de știință studiază aceste dimensiuni cu ajutorul analizei dimensionale.
Matematicienii folosesc, de asemenea, dimensiuni. În matematică, dimensiunile sunt mai generale. Este posibil ca dimensiunile din matematică să nu măsoare lucruri din lume. Regulile de calcul cu ajutorul dimensiunilor în matematică pot fi diferite de regulile aritmetice obișnuite.
Dimensiuni și vectori
Vectorii sunt utilizați pentru a indica distanțele și direcțiile. Vectorii sunt adesea utilizați în inginerie și în știință și, uneori, în matematică.
Un vector este o listă de numere. Există un număr pentru fiecare dimensiune. Există reguli aritmetice pentru vectori.
De exemplu, dacă Jane dorește să cunoască poziția lui Sally, Sally îi poate oferi lui Jane un vector care să indice poziția. Dacă Jane și Sally se află în lume, există trei dimensiuni. Prin urmare, Sally îi oferă lui Jane o listă de trei numere pentru a arăta poziția ei. Cele trei numere din vectorul pe care Sally i-l dă lui Jane pot fi:
- Distanța lui Sally la nord de Jane
- Distanța lui Sally la est de Jane
- Înălțimea lui Sally deasupra lui Jane
Pagini conexe
- 3D
- Hipercubul, generalizarea pătratului și cubului dincolo de trei dimensiuni
- Spațiu-timpul Minkowski, o mulțime cvadridimensională
- Spațiu-timp
Întrebări și răspunsuri
Î: Ce este o dimensiune?
R: O dimensiune este un mod de a măsura, de a vedea și de a experimenta lumea folosind concepte precum sus și jos, de la dreapta la stânga, de la spate la față, cald și rece, cât de greu și cât de lung. De asemenea, poate fi definită ca fiind gradele de libertate sau modul în care un obiect se poate mișca într-un anumit spațiu.
Î: Cum definesc matematicienii spațiul euclidian?
R: Matematicienii definesc spațiul euclidian ca fiind specificat de trei dimensiuni, care se numesc de obicei lungime, lățime și adâncime.
Î: Care este numărul de vectori într-un spațiu vectorial?
R: Numărul de vectori dintr-un spațiu vectorial este egal cu cardinalitatea (sau numărul de vectori) a setului său de bază.
Î: Câte dimensiuni sunt utilizate pentru a măsura poziția?
R: Pentru a măsura poziția se utilizează trei dimensiuni (lungime, lățime și înălțime). În unele ocazii, o a patra dimensiune (4D) - timpul - poate fi utilizată pentru a arăta poziția unui eveniment în timp și spațiu.
Î: Ce înseamnă dim(V)?
R: Dim(V) se referă la dimensiunea lui V, care este egală cu cardinalitatea (sau numărul de vectori) a setului său de bază sau egală cu numărul de direcții ale liniilor drepte pe care le are.
Î: Există o definiție care să satisfacă toate conceptele legate de dimensiuni?
R: Nu, nu există o singură definiție care să satisfacă toate conceptele legate de dimensiuni.
