Spațiu-timp Minkowski | o mulțime cu patru dimensiuni, creată de Hermann Minkowski
În relativitatea specială, spațiu-timpul Minkowski este o mulțime cvadridimensională, creată de Hermann Minkowski. Acesta are patru dimensiuni: trei dimensiuni spațiale (x, y, z) și o dimensiune temporală. Spațiu-timpul Minkowski are o semnătură metrică de (-+++) și descrie o suprafață plană atunci când nu există masă. Convenția din acest articol este de a numi spațiu-timp Minkowski pur și simplu spațiu-timp.
Cu toate acestea, spațiu-timpul Minkowski se aplică numai în relativitatea specială. Relativitatea generală a folosit noțiunea de spațiu-timp curbat pentru a descrie efectele gravitației și ale mișcării accelerate.
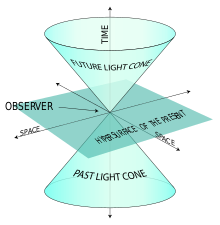
Exemplu de con de lumină.
Definiție(e)
Matematică
Spațiu-timpul poate fi considerat ca un sistem de coordonate cvadridimensional în care axele sunt date de
Ele pot fi, de asemenea, notate prin
Unde 

Aceasta implică faptul că spațiu-timpul are un tensor metric dat de
Așa cum am mai spus, spațiu-timpul este plat peste tot; într-o anumită măsură, poate fi considerat ca un plan.
Simplu
Spațiu-timpul poate fi considerat ca fiind "arena" în care se desfășoară toate evenimentele din univers. Tot ce este necesar pentru a specifica un punct în spațiu-timp este un anumit timp și o orientare spațială tipică. Este greu (practic imposibil) de vizualizat patru dimensiuni, dar se poate face o oarecare analogie, folosind metoda de mai jos.
Diagrame spațiu-timp
Hermann Minkowski a introdus o anumită metodă de reprezentare grafică a sistemelor de coordonate în spațiu-timpul Minkowski. După cum se vede în dreapta, diferite sisteme de coordonate nu vor fi de acord cu privire la orientarea spațială și/sau poziția în timp a unui obiect. După cum se poate observa din diagramă, există o singură axă spațială (axa x) și o singură axă a timpului (axa ct). Dacă este necesar, se poate introduce o dimensiune spațială suplimentară, (axa y); din păcate, aceasta este limita numărului de dimensiuni: graficarea în patru dimensiuni este imposibilă. Regula de reprezentare grafică în spațiu-timpul Minkowski este următoarea:
1) Unghiul dintre axa x și axa x' este dat de 
2) Viteza luminii prin spațiu-timp face întotdeauna un unghi de 45 de grade cu oricare dintre axe.
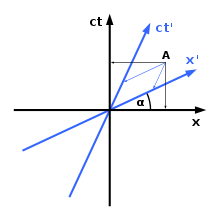
În teoria relativității, ambii observatori atribuie evenimentul de la A la momente diferite.
Spațiu-timp în relativitatea generală
În teoria generală a relativității, Einstein a folosit ecuația
Pentru a permite curbarea reală a spațiu-timpului; efectele rezultate sunt cele ale gravitației.
Pagini conexe
- Spațiu-timp
- Relativitatea specială
- Relativitatea generală
| Controlul autorității: Biblioteci naționale |
|
Întrebări și răspunsuri
Î: Ce este spațiu-timpul Minkowski?
R: Spațiu-timpul Minkowski este o mulțime cvadridimensională creată de Hermann Minkowski. Acesta are trei dimensiuni spațiale (x, y, z) și o dimensiune temporală.
Î: Care este semnătura metrică a spațiu-timpului Minkowski?
R: Semnătura metrică a spațiu-timpului Minkowski este (-+++).
Î: Cum descrie spațiu-timpul Minkowski o suprafață plană?
R: Atunci când nu există masă, spațiu-timpul Minkowski descrie o suprafață plană.
Î: Se aplică spațiu-timpul Minkowski relativității generale?
R: Nu, spațiul-timp Minkowski se aplică numai în relativitatea specială. Relativitatea generală utilizează noțiunea de spațiu-timp curbat pentru a descrie efectele gravitației și ale mișcării accelerate.
Î: Câte dimensiuni are spațiu-timpul Minkowski?
R: Spațiul-timp Minkowsi are patru dimensiuni - trei dimensiuni ale spațiului (x, y, z) și o dimensiune a timpului.
Î: Cine a creat conceptul de spațiu-timp Minkowsi?
R: Hermann Minkowksi a creat conceptul de spațiu-timp MInkowski.
Căuta în




