Vector euclidian | obiect matematic

Exemple de vectori

• John merge spre nord 20 de metri. Direcția "nord" împreună cu distanța "20 de metri" reprezintă un vector.
• Un măr cade cu 10 metri pe secundă. Direcția "în jos" combinată cu viteza "10 metri pe secundă" reprezintă un vector. Acest tip de vector se mai numește și viteză.

 

Exemple de scalari

• Distanța dintre două locuri este de 10 kilometri. Această distanță nu este un vector, deoarece nu conține o direcție.
• Numărul de fructe dintr-o cutie nu este un vector.
• O persoană care arată cu degetul nu este un vector, deoarece există doar o direcție. Nu există o mărime (distanța de la degetul persoanei la o clădire, de exemplu).
• Lungimea unui obiect.
• O mașină circulă cu 100 de kilometri pe oră. Acest lucru nu descrie un vector, deoarece există doar o mărime, dar nu și o direcție.

 

Alte exemple de vectori

• Deplasarea este un vector. Deplasarea este distanța pe care se deplasează ceva într-o anumită direcție. O măsură a distanței singură este un scalar.
• Forța care include direcția este un vector.
• Viteza este un vector, deoarece este o viteză într-o anumită direcție.
• Accelerația este rata de schimbare a vitezei. Un obiect accelerează dacă își schimbă viteza sau își schimbă direcția.

 

Cum se adaugă vectori

Adăugarea vectorilor pe hârtie folosind metoda cap-coadă

Metoda de adunare a vectorilor de la cap la coadă este utilă pentru a face o estimare pe hârtie a rezultatului adunării a doi vectori. Pentru a face acest lucru:

• Fiecare vector este desenat ca o săgeată cu o lungime în spatele ei, unde fiecare unitate de lungime de pe hârtie reprezintă o anumită mărime a vectorului.
• Desenați următorul vector, cu coada (capătul) celui de-al doilea vector la capul (fața) primului vector.
• Se repetă pentru toți ceilalți vectori: Desenați coada vectorului următor la capul vectorului anterior.
• Trageți o linie de la coada primului vector până la capul ultimului vector - aceasta este rezultanta (suma) tuturor vectorilor.

Se numește metoda "Cap la coadă", deoarece fiecare cap din vectorul anterior conduce la coada vectorului următor.

Utilizarea formularului de componente

^{[trebuie să fie explicat ]}

Utilizarea formei componente pentru a adăuga doi vectori înseamnă, la propriu, adăugarea componentelor vectorilor pentru a crea un nou vector. De exemplu, fie a și b doi vectori bidimensionali. Acești vectori pot fi scriși în funcție de componentele lor.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})}

Să presupunem că c este suma acestor doi vectori, astfel încât c = a + b. Aceasta înseamnă că c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

Iată un exemplu de adunare a doi vectori, folosind formele lor componente:

a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)}

b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)}

c = a + b = ( a x + b x , a y + b y ) = ( 3 + 2 , - 1 + 2 ) = ( 5 , 1 ) {\displaystyle {\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}}

Această metodă funcționează pentru toți vectorii, nu doar pentru cei bidimensionali.

 
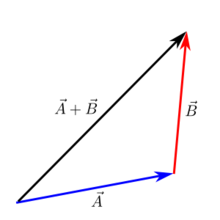
Adăugare cap-coadă  

Cum se înmulțesc vectorii

Folosind produsul punct

Produsul punct este o metodă de multiplicare a vectorilor. Acesta produce un scalar. Folosește forma componentă:

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\displaystyle {\begin{aligned}\mathbf {a} &=(2,3)\\\mathbf {b} &=(1,4)\\mathbf {a} \cdot \mathbf {b} &=(2,3)\cdot (1,4)\&=(2\cdot 1)+(3\cdot 4)\&=2+12\\\&=14\end{aligned}}}}

Folosind produsul încrucișat

Produsul încrucișat este o altă metodă de multiplicare a vectorilor. Spre deosebire de produsul punct, acesta produce un vector. Se utilizează forma componentă:

a × b = | a | a | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} |||mathbf {b} \sin(\theta )\mathbf {n} }

Aici, | a | a | {\displaystyle |\mathbf {a} |} înseamnă lungimea unui {\displaystyle \mathbf {a} } și n {\displaystyle \mathbf {n} } reprezintă vectorul unitar în unghiuri drepte față de ambele {\displaystyle \mathbf {a}. } și b {\displaystyle \mathbf {b} } .

Înmulțirea cu un scalar

Pentru a înmulți un vector cu un scalar (un număr normal), se înmulțește numărul cu fiecare componentă a vectorului:

c x = ( c x 1 , c x 2 , . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})}

Un exemplu în acest sens este

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\displaystyle {\begin{aligned}c&=5\\\\mathbf {x} &=(3,4)\c\,\mathbf {x} &=(5\cdot 3,5\cdot 4)\\\&=(15,20)\end{aligned}}}}}

 

Pagini conexe

• Geometrie analitică
• Vector nul
• Vector unitar
• Câmp vectorial
• Grafică vectorială
• Spațiul vectorial
• Subspațiu vectorial