Produsul punctului

Definiție

Produsul punctat a doi vectori a = [a₁ , a₂ , ..., a_n ] și b = [b₁ , b₂ , ..., b_n ] se definește astfel:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}}{n}}}

unde Σ reprezintă notația de adunare ( suma tuturor termenilor) și n este dimensiunea spațiului vectorial.

În dimensiunea 2, produsul punctat al vectorilor [a,b] și [c,d] este ac + bd. În același mod, într-o dimensiune 3, produsul punct al vectorilor [a,b,c] și [d,e,f] este ad + be + cf. De exemplu, produsul punct al doi vectori tridimensionali [1, 3, -5] și [4, -2, -1] este

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\ ori 4)+(3\ ori (-2))+((-5)\ ori (-1))=(4)-(6)+(5)=3.}

Interpretarea geometrică

În geometria euclidiană, produsul punctului, lungimea și unghiul sunt legate între ele. Pentru un vector a, produsul punct a - a este pătratul lungimii lui a, sau

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\||\mathbf {a} \right\|^{2}}

unde ||a||| reprezintă lungimea (mărimea) lui a. Mai general, dacă b este un alt vector

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\\\|\,\left\||\mathbf {b} \right\\\ \cos \theta \,}

unde ||a||| și ||b||| semnifică lungimea lui a și b, iar θ este unghiul dintre ele.

Această formulă poate fi rearanjată pentru a determina mărimea unghiului dintre doi vectori care nu sunt zero:

θ = arccos ( a ⋅ b ‖ a ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\drept\|\left\|{\mathbf {b}}\}\drept\}}}}}\}drept)}

De asemenea, se pot converti mai întâi vectorii în vectori unitari prin împărțirea la mărimea lor:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\}|}}}}}}

atunci unghiul θ este dat de

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}}\cdot {\boldsymbol {\hat {b}}})}

Deoarece cosinusul a 90° este zero, produsul punct al doi vectori ortogonali (perpendiculari) este întotdeauna zero. Mai mult, doi vectori pot fi considerați ortogonali dacă și numai dacă produsul lor în puncte este zero și dacă ambii au o lungime diferită de zero. Această proprietate oferă o metodă simplă de a testa condiția de ortogonalitate.

Uneori, aceste proprietăți sunt utilizate și pentru a defini produsul punct, în special în 2 și 3 dimensiuni; această definiție este echivalentă cu cea de mai sus. Pentru dimensiuni mai mari, formula poate fi utilizată pentru a defini conceptul de unghi.

Proprietățile geometrice se bazează pe faptul că baza este ortonormată, adică compusă din vectori perpendiculari pe perechi cu lungime unitară.

Proiecție scalară

Dacă atât a cât și b au lungimea unu (adică sunt vectori unitari), produsul lor în puncte dă pur și simplu cosinusul unghiului dintre ele.

Dacă numai b este un vector unitar, atunci produsul punctat a - b dă |a| cos(θ), adică mărimea proiecției lui a în direcția lui b, cu semnul minus dacă direcția este opusă. Aceasta se numește proiecția scalară a lui a pe b sau componenta scalară a lui a în direcția lui b (a se vedea figura). Această proprietate a produsului punct are mai multe aplicații utile (de exemplu, a se vedea secțiunea următoare).

Dacă nici a, nici b nu sunt vectori unitari, atunci mărimea proiecției lui a în direcția lui b, de exemplu, ar fi a - (b / |b|), deoarece vectorul unitar în direcția lui b este b / |b|.

Rotație

O rotație a bazei ortonormale în funcție de care este reprezentat vectorul a se obține prin înmulțirea lui a cu o matrice de rotație R. Această înmulțire a matricei este doar o reprezentare compactă a unei secvențe de produse de puncte.

De exemplu, fie

• B₁ = {x, y, z} și B₂ = {u, v, w} să fie două baze ortonormale diferite ale aceluiași spațiu R³ , B₂ fiind obținută prin simpla rotire a lui B₁ ,
• a₁ = (a_x , a_y , a_z ) reprezintă vectorul a în termenii lui B₁ ,
• a₂ = (a_u , a_v , a_w ) reprezintă același vector în termenii bazei rotite B₂ ,
• u₁ , v₁ , w₁ să fie vectorii de bază rotiți u, v, w reprezentați în termenii lui B₁ .

Apoi, rotația de la B₁ la B₂ se efectuează după cum urmează:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}}_{1}\cdot {\mathbf {a}}_{1}\\\{mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\a_{v}\a_{w}\end{bmatrix}}. }

Observați că matricea de rotație R este asamblată prin utilizarea vectorilor de bază rotiți u₁ , v₁ , w₁ ca rânduri ale acesteia, iar acești vectori sunt vectori unitari. Prin definiție, Ra₁ constă într-o secvență de produse de puncte între fiecare dintre cele trei rânduri ale lui R și vectorul a₁ . Fiecare dintre aceste produse de puncte determină o componentă scalară a lui a în direcția unui vector de bază rotit (a se vedea secțiunea anterioară).

Dacă un₁ este un vector de rând, mai degrabă decât un vector de coloană, atunci R trebuie să conțină vectorii de bază rotiți în coloanele sale și trebuie să post-multiplice un₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={{\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

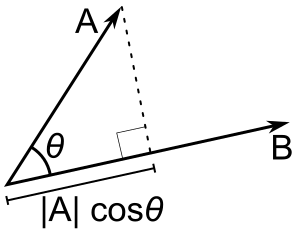
A - B = |A| |B| cos(θ). |A| cos(θ) este proiecția scalară a lui A pe B.

Fizică

În fizică, magnitudinea este un scalar în sens fizic, adică o mărime fizică independentă de sistemul de coordonate, exprimată ca produs dintre o valoare numerică și o unitate fizică, nu doar un număr. Produsul punct este, de asemenea, un scalar în acest sens, dat de formula, independent de sistemul de coordonate. Exemplu:

• Lucrul mecanic este produsul punctat al vectorilor forță și deplasare.
• Fluxul magnetic este produsul punct al câmpului magnetic și al vectorilor de suprafață.
• Debitul volumetric este produsul punctat al vectorilor de viteză și de suprafață ai fluidului.

Proprietăți

Următoarele proprietăți sunt valabile dacă a, b și c sunt vectori reali și r este un scalar.

Produsul punct este comutativ:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

Produsul punct este distributiv față de adunarea vectorială:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} + \mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

Produsul punct este biliniar:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Atunci când este înmulțit cu o valoare scalară, produsul punct satisface:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(aceste ultime două proprietăți decurg din primele două).

Doi vectori nenule a și b sunt perpendiculare dacă și numai dacă a - b = 0.

Spre deosebire de înmulțirea numerelor obișnuite, unde dacă ab = ac, atunci b este întotdeauna egal cu c, cu excepția cazului în care a este zero, produsul punct nu respectă legea anulării:

Dacă a - b = a - c și a ≠ 0, atunci putem scrie: a - (b - c) = 0 prin legea distributivă; rezultatul de mai sus spune că acest lucru înseamnă doar că a este perpendicular pe (b - c), ceea ce permite ca (b - c) ≠ 0 și, prin urmare, b ≠ c.

Cu condiția ca baza să fie ortonormală, produsul punctelor este invariant în cazul unor modificări izometrice ale bazei: rotații, reflexii și combinații, cu menținerea originii fixe. Interpretarea geometrică menționată mai sus se bazează pe această proprietate. Cu alte cuvinte, pentru un spațiu ortonormal cu orice număr de dimensiuni, produsul punctual este invariant în cazul unei transformări de coordonate bazate pe o matrice ortogonală. Acest lucru corespunde următoarelor două condiții:

• Noua bază este din nou ortonormală (adică este ortonormală exprimată în cea veche).
• Noii vectori de bază au aceeași lungime cu cei vechi (adică lungime unitară în raport cu vechea bază).

Dacă a și b sunt funcții, atunci derivata lui a - b este a' - b + a - b'.

Extinderea produsului triplu

Aceasta este o identitate foarte utilă (cunoscută și sub numele de formula lui Lagrange) care implică produsul punctelor și produsul încrucișat. Ea se scrie sub forma

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

care este mai ușor de reținut ca "BAC minus CAB", ținând cont de vectorii care sunt punctați împreună. Această formulă este utilizată în mod obișnuit pentru a simplifica calculele vectoriale în fizică.

Dovada interpretării geometrice

Se consideră elementul din R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Prin aplicarea repetată a teoremei lui Pitagora se obține pentru lungimea sa |v|

| v | 2 = v 1 2 + v 2 2 + . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Dar acest lucru este același lucru cu

v ⋅ v = v 1 2 + v 2 2 + . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

astfel încât să concluzionăm că dacă luăm produsul punct al unui vector v cu el însuși, obținem lungimea la pătrat a vectorului.

Lema 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Considerăm acum doi vectori a și b care se extind de la origine, separați de un unghi θ. Un al treilea vector c poate fi definit astfel

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {\mathrm {def} }{=}}}\ \mathbf {a} -\mathbf {b} .\,}

creând un triunghi cu laturile a, b și c. Conform legii cosinusurilor, avem

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} |||mathbf {b} \cos \theta .\,}

Înlocuind produsele de puncte pentru lungimile pătrate conform Lema 1, obținem

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} |||mathbf {b} |\cos \theta .\,} (1)

Dar, cum c ≡ a - b, avem de asemenea

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

care, în conformitate cu legea distributivă, se extinde la

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

Unind cele două ecuații c - c, (1) și (2), obținem

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b}. \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} | |||mathbf {b} \cos \theta .\,}

Scăzând a - a + b - b - b din ambele părți și împărțind la -2 rezultă

a ⋅ b = | a | b | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} |||mathbf {b} \cos \theta .\,}

Q.E.D.

Generalizare

Produsul interior generalizează produsul punct la spațiile vectoriale abstracte și este de obicei notat prin ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . Datorită interpretării geometrice a produsului punct, norma ||a||| a unui vector a într-un astfel de spațiu de produs intern este definită ca fiind

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={sqrt {\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}}

astfel încât să generalizeze lungimea, iar unghiul θ dintre doi vectori a și b de către

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b}  \|}}. }

În special, doi vectori sunt considerați ortogonali dacă produsul lor interior este zero.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

Pentru vectorii cu intrări complexe, utilizarea definiției date a produsului punct ar conduce la proprietăți geometrice foarte diferite. De exemplu, produsul punct al unui vector cu el însuși poate fi un număr complex arbitrar și poate fi zero fără ca vectorul să fie vectorul zero; acest lucru ar avea, la rândul său, consecințe grave asupra unor noțiuni precum lungimea și unghiul. Multe proprietăți geometrice pot fi salvate, cu prețul renunțării la proprietățile simetrice și biliniare ale produsului scalar, prin definirea alternativă a următoarelor elemente

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

unde b_i este conjugatul complex al lui b_i . Atunci produsul scalar al oricărui vector cu el însuși este un număr real nenegativ și este nenul, cu excepția vectorului zero. Cu toate acestea, acest produs scalar nu este liniar în b (ci mai degrabă liniar conjugat), iar produsul scalar nu este nici simetric, deoarece

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}}} .

Acest tip de produs scalar este totuși destul de util și conduce la noțiunile de formă hermitiană și de spații cu produs interior general.

Produsul interior Frobenius generalizează produsul punct la matrici. Acesta se definește ca fiind suma produselor componentelor corespunzătoare a două matrici de aceeași mărime.

Generalizare la tensori

Produsul punctual dintre un tensor de ordin n și un tensor de ordin m este un tensor de ordin n+m-2. Produsul punctat se calculează prin înmulțirea și adunarea unui singur indice din ambii tensori. Dacă A {\displaystyle \mathbf {A} } și B {\displaystyle \mathbf {B} } sunt doi tensori cu reprezentarea elementelor A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} și B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} elementele produsului punctual A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } sunt date de

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}^{p{\dots }i}}.

Această definiție se reduce în mod natural la produsul standard de puncte vectorial atunci când se aplică vectorilor și la înmulțirea matricelor atunci când se aplică matricelor.

Ocazional, se utilizează un produs dublu de puncte pentru a reprezenta înmulțirea și adunarea a doi indici. Produsul dublu punctat între doi tensori de ordinul 2 este un scalar.

Pagini conexe

• Inegalitatea Cauchy-Schwarz
• Produs încrucișat
• Înmulțirea matricelor
• Fizică