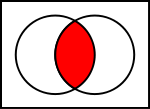
Diagramă Venn | diagramă care arată relația logică dintre seturi

O diagramă Venn este o diagramă care arată relația logică dintre seturi. Acestea au fost popularizate de John Venn în anii 1880 și sunt utilizate pe scară largă în prezent. Ele sunt utilizate pentru a preda teoria elementară a seturilor și pentru a ilustra relațiile simple dintre seturi în probabilitate, logică, statistică, lingvistică și informatică. O diagramă Venn utilizează curbe închise desenate pe un plan pentru a reprezenta seturi. Foarte adesea, aceste curbe sunt cercuri sau elipse.

Idei similare fuseseră propuse înainte de Venn. Christian Weise în 1712 (Nucleus Logicoe Wiesianoe) și Leonhard Euler (Scrisori către o prințesă germană) în 1768, de exemplu, au venit cu idei similare. Ideea a fost popularizată de Venn în Logica simbolică, capitolul V "Reprezentarea schematică", 1881.

Vitraliu din Cambridge, unde a studiat John Venn. Acesta prezintă o diagramă Venn.

Exemplu

Exemplul următor utilizează două seturi, A și B, reprezentate aici prin cercuri colorate. Cercul portocaliu, setul A, reprezintă toate ființele vii cu două picioare. Cercul albastru, setul B, reprezintă ființele vii care pot zbura. Fiecare tip separat de creatură poate fi imaginat ca un punct undeva în diagramă. Creaturile vii care pot zbura și care au două picioare - de exemplu, papagalii - se regăsesc în ambele seturi și, prin urmare, corespund punctelor din zona în care cercurile albastru și portocaliu se suprapun. Acea zonă conține toate (și numai) astfel de ființe vii.

Oamenii și pinguinii sunt bipede și, prin urmare, se află în cercul portocaliu, dar, deoarece nu pot zbura, apar în partea stângă a cercului portocaliu, unde nu se suprapune cu cercul albastru. Țânțarii au șase picioare și zboară, deci punctul pentru țânțari se află în partea cercului albastru care nu se suprapune cu cel portocaliu. Creaturile care nu au două picioare și nu pot zbura (de exemplu, balenele și păianjenii) ar fi reprezentate de puncte în afara ambelor cercuri.

Suprafața combinată a seturilor A și B se numește uniunea dintre A și B, notată cu A ∪ B. În acest caz, uniunea conține toate creaturile vii care au fie două picioare, fie pot zbura (sau ambele). Zona din A și B, în care cele două seturi se suprapun, se numește intersecția dintre A și B, notată cu A ∩ B. De exemplu, intersecția celor două seturi nu este goală, deoarece există puncte care reprezintă creaturi care se află atât în cercul portocaliu, cât și în cel albastru.

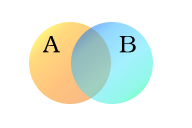
Seturile A (creaturi cu două picioare) și B (creaturi care pot zbura)

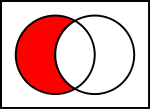
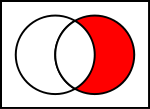
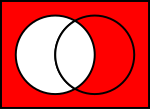
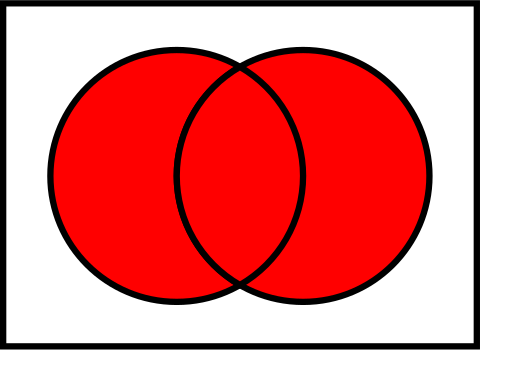
Diagrame Venn ale operațiilor comune asupra seturilor

În ilustrațiile de mai jos, cercul din stânga arată setul A {\displaystyle A} $A$ și cercul din dreapta arată setul B {\displaystyle B} $B$ . Rezultatele operațiilor sunt prezentate sub formă de zone colorate.

Diferență A ∖ B {\displaystyle A\setminus B} $A\setminus B$

Diferență B ∖ A {\displaystyle B\setminus A} $B\setminus A$

Complementul lui A A A C = U ∖ A {\displaystyle A^{\rm {C}}=U\setminus A} $A^{\rm {C}}=U\setminus A$

Union A ∪ B {\displaystyle A\cup B} $A\cup B$

Intersecție A ∩ B {\displaystyle A\cap B} $A\cap B$

Pagini conexe

Disjuncție exclusivă
Disjuncție incluzivă

Întrebări și răspunsuri

Î: Ce este o diagramă Venn?

R: O diagramă Venn este o diagramă care arată relația logică dintre seturi. Ea utilizează curbe închise desenate pe un plan, de obicei cercuri sau elipse, pentru a reprezenta seturi.

Î: Cine a popularizat diagramele Venn?

R: John Venn a popularizat diagramele Venn în anii 1880.

Î: La ce sunt utilizate?

R: Ele sunt utilizate pentru a preda teoria elementară a seturilor și pentru a ilustra relații simple între seturi în probabilitate, logică, statistică, lingvistică și informatică.

Î: Cine a propus idei similare înainte de John Venn?

R: Christian Weise a propus idei similare în 1712 cu Nucleus Logicoe Wiesianoe, iar Leonhard Euler le-a propus în Scrisori către o prințesă germană în 1768.

Î: Când a publicat John Venn Logica simbolică?

R: John Venn a publicat Symbolic Logic în 1881.

Î: În ce capitol din Symbolic Logic a fost popularizată ideea de diagramă Venn de către John Venn?

R: Ideea de diagramă Venn a fost popularizată de John Venn în capitolul 5 "Reprezentarea diagramatică" din Logica simbolică.

Î: Cum erau reprezentate aceste idei înainte de inventarea versiunii moderne a diagrameiV enn?

R: Înainte de inventarea versiunii moderne a diagrameiV enn, aceste idei erau reprezentate cu ajutorul unor curbe închise desenate pe un plan, cum ar fi cercuri sau elipse.