Teorema schemei lui Holland

Teorema schemei lui Holland, numită și teorema fundamentală a algoritmilor genetici, este o inegalitate care rezultă din gradația grosieră a unei ecuații pentru dinamica evolutivă. Teorema schemelor spune că schemele scurte, de ordin inferior, cu o fitness peste medie, cresc exponențial în frecvență în generații succesive. Teorema a fost propusă de John Holland în anii 1970. Inițial, a fost considerată pe scară largă ca fiind fundamentul explicațiilor privind puterea algoritmilor genetici. Cu toate acestea, această interpretare a implicațiilor sale a fost criticată în mai multe publicații analizate în , unde se arată că teorema schemelor este un caz special al ecuației lui Price cu funcția indicatoare a schemelor ca măsură macroscopică.

O schemă este un șablon care identifică un subset de șiruri de caractere cu similitudini în anumite poziții. Schemele sunt un caz special de seturi cilindrice și, prin urmare, formează un spațiu topologic.

Descriere

Se consideră șiruri binare de lungime 6. Schema 1*10*1 descrie ansamblul tuturor șirurilor de lungime 6 cu 1 în pozițiile 1, 3 și 6 și cu 0 în poziția 4. * este un simbol joker, ceea ce înseamnă că pozițiile 2 și 5 pot avea o valoare de 1 sau 0. Ordinea unei scheme o ( H ) {\displaystyle o(H)} $o(H)$ este definită ca fiind numărul de poziții fixe din șablon, în timp ce lungimea definitorie δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ este distanța dintre prima și ultima poziție specifică. Ordinea lui 1*10*1 este 4, iar lungimea sa definitorie este 5. Fitness-ul unei scheme este fitness-ul mediu al tuturor șirurilor care corespund schemei. Fitness-ul unui șir este o măsură a valorii soluției codificate a problemei, calculată cu ajutorul unei funcții de evaluare specifice problemei. Utilizând metodele și operatorii genetici consacrați ai algoritmilor genetici, teorema schemelor afirmă că schemele scurte, de ordin inferior, cu o fitness peste medie, cresc exponențial în generații succesive. Exprimată sub forma unei ecuații:

E ( m ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \ peste a_{t}}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Aici m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ este numărul de șiruri aparținând schemei H {\displaystyle H} $H$ la generația t {\displaystyle t}. $t$ , f ( H ) {\displaystyle f(H)} $f(H)$ este fitnessul mediu observat al schemei H {\displaystyle H} $H$ și a t {\displaystyle a_{t}} $a_{t}$ este fitnessul mediu observat la generația t {\displaystyle t} $t$ . Probabilitatea de întrerupere p {\displaystyle p} $p$ este probabilitatea ca încrucișarea sau mutația să distrugă schema H {\displaystyle H} $H$ . Ea poate fi exprimată astfel:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

unde o ( H ) {\displaystyle o(H)} $o(H)$ este ordinea schemei, l {\displaystyle l} $l$ este lungimea codului, p m {\displaystyle p_{m}} $p_{m}$ este probabilitatea de mutație și p c {\displaystyle p_{c}} $p_{c}$ este probabilitatea de încrucișare. Așadar, o schemă cu o lungime de definire mai mică δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ are mai puține șanse de a fi perturbată.
Un aspect adesea neînțeles este motivul pentru care teorema schemei este o inegalitate și nu o egalitate. Răspunsul este, de fapt, simplu: Teorema neglijează probabilitatea mică, dar diferită de zero, ca un șir aparținând schemei H {\displaystyle H} $H$ să fie creat "de la zero" prin mutația unui singur șir (sau recombinarea a două șiruri) care nu aparținea lui H {\displaystyle H} $H$ în generația anterioară.

Limitare

Teorema schemelor este valabilă în ipoteza unui algoritm genetic care menține o populație infinit de mare, dar nu se aplică întotdeauna în practică (finită): din cauza erorilor de eșantionare din populația inițială, algoritmii genetici pot converge la scheme care nu au niciun avantaj selectiv. Acest lucru se întâmplă în special în optimizarea multimodală, unde o funcție poate avea mai multe vârfuri: populația poate derapa pentru a prefera unul dintre vârfuri, ignorându-le pe celelalte.

Motivul pentru care Teorema Schemei nu poate explica puterea algoritmilor genetici este că aceasta este valabilă pentru toate cazurile de probleme și nu poate face distincția între problemele în care algoritmii genetici au performanțe slabe și problemele în care algoritmii genetici au performanțe bune.

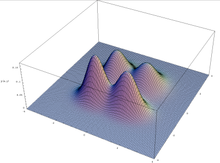
Reprezentarea grafică a unei funcții multimodale în două variabile.

Întrebări și răspunsuri

Î: Ce este teorema schemei lui Holland?

R: Teorema schemei lui Holland este o teoremă referitoare la algoritmii genetici care spune că indivizii cu o fitness mai mare decât media au mai multe șanse să prevaleze.

Î: Cine și când a propus teorema schemei lui Holland?

R: John Holland a propus teorema schemei lui Holland în anii 1970.

Î: Ce este o schemă în contextul algoritmilor genetici?

R: În contextul algoritmilor genetici, o schemă este un șablon care identifică un subansamblu de șiruri de caractere cu asemănări în anumite poziții ale acestora.

Î: Care este interpretarea teoremei schemelor lui Holland care a fost folosită ca bază pentru explicațiile privind puterea algoritmilor genetici?

R: Interpretarea teoremei schemelor lui Holland, care a fost utilizată ca bază pentru explicațiile privind puterea algoritmilor genetici, este că indivizii cu o fitness mai mare decât media au mai multe șanse de a învinge.

Î: Ce au arătat criticile aduse teoremei schemei lui Holland?

R: Criticile aduse teoremei schemei lui Holland au arătat că aceasta este un caz special al ecuației lui Price cu funcția indicatoare a schemei ca măsură macroscopică.

Î: Care este un caz special de seturi cilindrice?

R: Schemele sunt un caz special de seturi cilindrice.

Î: Ce fel de spațiu formează schemele?

R: Schemele formează un spațiu topologic.