Funcția Heaviside
Funcția Heaviside, H este o funcție necontinuă a cărei valoare este zero pentru o intrare negativă și unu pentru o intrare pozitivă.
Funcția este utilizată în matematica teoriei controlului pentru a reprezenta un semnal care se activează la un moment specificat și rămâne activat pe o perioadă nedeterminată. A fost numită după englezul Oliver Heaviside.
Funcția Heaviside este integrala funcției delta Dirac: H′ = δ. Aceasta se scrie uneori sub forma
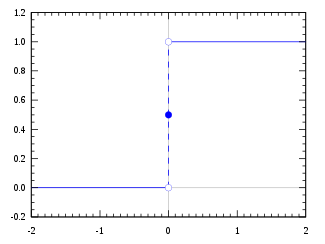
Funcția de pas Heaviside, folosind convenția de semimaximă
Forma discretă
De asemenea, putem defini o formă alternativă a funcției de pas Heaviside ca funcție a unei variabile discrete n:
H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\displaystyle H[n]={\begin{cases}0,&n<0\\\1,&n\geq 0\end{cases}}}}}
unde n este un număr întreg.
Sau
H ( x ) = lim z → x - ( ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)}
Impulsul unitar în timp discret este prima diferență a pasului în timp discret
δ [ n ] = H [ n ] - H [ n - 1 ] . {\displaystyle \delta \left[n\right]=H[n]-H[n-1]. }
Această funcție este suma cumulativă a delta Kronecker:
H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}
unde
δ [ k ] = δ k , 0 {\displaystyle \delta [k]=\delta _{k,0}\,}
este funcția de impuls unitar discret.
Reprezentări
Adesea este utilă o reprezentare integrală a funcției de pas Heaviside:
H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ 1 τ - i ϵ e i x τ τ d τ . {\displaystyle H(x)=\lim _{\epsilon \to 0^{+}}-{1 \ peste 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \ peste \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{{\epsilon \to 0^{+}}{1 \ peste 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau . } 
H(0)
Valoarea funcției la 0 poate fi definită ca H(0) = 0, H(0) = ½ sau H(0) = 1.
H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} 
Pagini conexe
- Transformată Laplace
Întrebări și răspunsuri
Î: Ce este funcția Heaviside?
R: Funcția Heaviside este o funcție necontinuă a cărei valoare este zero pentru o intrare negativă și unu pentru o intrare pozitivă.
Î: De ce este utilizată funcția Heaviside în teoria controlului?
R: Funcția Heaviside este utilizată în teoria controlului pentru a reprezenta un semnal care se activează la un moment specificat și rămâne activat pe termen nelimitat.
Î: Cine este persoana după care a fost numită funcția Heaviside?
R: Funcția Heaviside a fost numită după englezul Oliver Heaviside.
Î: Care este relația dintre funcția Heaviside și funcția delta Dirac?
R: Funcția Heaviside este integrala funcției delta Dirac: H′(x)= δ(x).
Î: Care este rezultatul funcției Heaviside pentru intrări pozitive?
R: Funcția Heaviside produce unu pentru intrări pozitive.
Î: Care este rezultatul funcției Heaviside pentru intrări negative?
R: Funcția Heaviside produce zero pentru intrări negative.
Î: Ce tip de funcție este funcția Heaviside?
R: Funcția Heaviside este o funcție necontinuă.
Căuta în
![{\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}](https://www.alegsaonline.com/image/efb65c686bdec46712eae1997c363f7ef8709b79.svg)

![{\displaystyle \delta \left[n\right]=H[n]-H[n-1].}](https://www.alegsaonline.com/image/e6c417f161a7987a4db18818743eeb23494b0feb.svg)
![{\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}](https://www.alegsaonline.com/image/5db28db3163e2940aaf93d0fc180edb19d865d32.svg)
![{\displaystyle \delta [k]=\delta _{k,0}\,}](https://www.alegsaonline.com/image/97a99ab7d257c74f38fbb2d42c8e42e1cb16d0e9.svg)