Spațiul de probabilitate
Spațiul de probabilitate este un model matematic utilizat pentru a descrie experimentele științifice Un spațiu de probabilitate este format din trei părți:
- Un spațiu de eșantionare care enumeră toate rezultatele posibile
- Un set de evenimente. Fiecare eveniment asociază zero sau mai multe rezultate
- O funcție care atribuie probabilități fiecărui eveniment
Un rezultat este rezultatul unei singure execuții a modelului. Deoarece rezultatele individuale ar putea avea o utilitate practică redusă, se utilizează evenimente mai complexe pentru a caracteriza grupuri de rezultate. Colecția tuturor acestor evenimente este o σ-algebră F {\displaystyle \scriptstyle {\mathcal {F}}}. 
. În cele din urmă, este necesar să se precizeze probabilitatea de apariție a fiecărui eveniment. Acest lucru se face cu ajutorul funcției de măsurare a probabilității, P.
Odată stabilit spațiul de probabilitate, se presupune că "natura" își face mișcarea și selectează un singur rezultat, ω, din spațiul de eșantionare Ω. Se spune că toate evenimentele din F {\displaystyle \scriptstyle {\mathcal {F}}} care conțin rezultatul selectat ω (reamintim că fiecare eveniment este un subansamblu al lui Ω) sunt considerate ca "au avut loc". Selecția efectuată de natură se face în așa fel încât, dacă experimentul ar fi repetat de un număr infinit de ori, frecvențele relative de apariție ale fiecăruia dintre evenimente ar coincide cu probabilitățile prescrise de funcția P.
Matematicianul sovietic proeminent Andrey Kolmogorov a introdus noțiunea de spațiu de probabilitate, împreună cu alte axiome ale probabilității, în anii 1930.
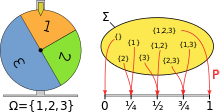
Modelarea unei roți a norocului folosind spațiul de probabilitate
Întrebări și răspunsuri
Î: Ce este un spațiu de probabilitate?
R: Un spațiu de probabilitate este un model matematic utilizat pentru a descrie experimentele științifice. Acesta este format din trei părți: un spațiu de eșantionare care enumeră toate rezultatele posibile, un set de evenimente care asociază zero sau mai multe rezultate și o funcție care atribuie probabilități fiecărui eveniment.
Î: Din ce este format spațiul de eșantionare?
R: Spațiul de eșantionare este format din toate rezultatele posibile, deseori scris ca Ω {\displaystyle \Omega } , și un rezultat ca ω {\displaystyle \omega } .
Î: Ce este un rezultat?
R: Un rezultat este rezultatul unei singure execuții a modelului.
Î: La ce sunt utilizate evenimentele în spațiile de probabilitate?
R: Evenimentele sunt utilizate pentru a caracteriza grupuri de rezultate, deoarece rezultatele individuale ar putea fi de puțin folos practic. Colecția tuturor acestor evenimente se numește σ-algebră, uneori scrisă ca F {\displaystyle {\mathcal {F}}} .
Î: Cum se atribuie probabilitățile fiecărui eveniment?
R: Probabilitățile sunt atribuite fiecărui eveniment cu ajutorul funcției de măsurare a probabilității P.
Î: Cine a introdus noțiunea de spații de probabilitate? R: Matematicianul sovietic proeminent Andrey Kolmogorov a introdus noțiunea de spații de probabilitate împreună cu alte axiome ale probabilității în anii 1930.
