Postulatul paralel
În geometrie, postulatul paralelismului este una dintre axiomele geometriei euclidiene. Uneori este numit și al cincilea postulat al lui Euclid, deoarece este cel de-al cincilea postulat din Elementele lui Euclid.
Postulatul spune că:
Dacă tăiați un segment de dreaptă cu două drepte, iar cele două unghiuri interioare pe care le formează dreptele sunt mai mici de 180°, atunci cele două drepte se vor întâlni în cele din urmă dacă le prelungiți suficient de mult.
Domeniul geometriei care respectă toate axiomele lui Euclid se numește geometrie euclidiană. Geometriile care nu respectă toate axiomele lui Euclid se numesc geometrie neeuclidiană.
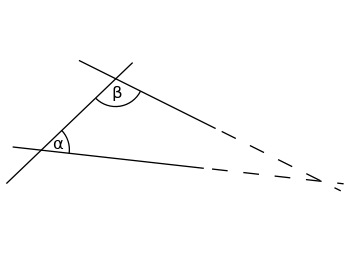
Dacă suma unghiurilor interioare α (alfa) și β (beta) este mai mică de 180°, cele două drepte se vor intersecta undeva, dacă ambele sunt prelungite la infinit.
Istoric
Unii matematicieni au considerat că al cincilea postulat al lui Euclid era mult mai lung și mai complicat decât celelalte patru postulate. Mulți dintre ei au crezut că acesta putea fi demonstrat pornind de la celelalte axiome mai simple. Unii matematicieni au anunțat că au demonstrat postulatul pornind de la propozițiile mai simple, dar toți s-au dovedit a fi în eroare.
Axioma lui Playfair
O altă propoziție mai recentă, cunoscută sub numele de axioma lui Playfair, este similară celui de-al cincilea postulat al lui Euclid. Aceasta spune că:
Dacă se dă o dreaptă și un punct care nu se află pe această dreaptă, se poate trasa doar o singură dreaptă prin acest punct care nu se va întâlni cu cealaltă dreaptă.
De fapt, matematicienii au descoperit că această axiomă nu numai că este similară cu cel de-al cincilea postulat al lui Euclid, dar are exact aceleași implicații. Din punct de vedere matematic, cele două propoziții se numesc propoziții "echivalente". Astăzi, axioma lui Playfair este folosită mai des de matematicieni decât postulatul paralel original al lui Euclid.
Geometrie neeuclidiană
În cele din urmă, unii matematicieni au încercat să construiască noi geometrii fără a utiliza axioma. Un tip de geometrie neeuclidiană se numește geometrie eliptică. În geometria eliptică postulatul paralelismului este înlocuit cu o axiomă care afirmă că:
Având o dreaptă și un punct care nu se află pe această dreaptă, nu se poate trasa o dreaptă prin acest punct care să nu intersecteze în cele din urmă cealaltă dreaptă.
Matematicienii au descoperit că, atunci când au înlocuit al cincilea postulat al lui Euclid cu această axiomă, au reușit să demonstreze în continuare multe dintre celelalte teoreme ale lui Euclid. Un mod de a ne imagina geometria eliptică este să ne gândim la suprafața unui glob pământesc. Pe un glob, liniile de longitudine par a fi paralele la ecuator, dar toate se întâlnesc la poli. La sfârșitul secolului al XIX-lea, s-a demonstrat că geometria eliptică este coerentă. Acest lucru a demonstrat că al cincilea postulat al lui Euclid nu era independent de celelalte postulate. După aceasta, matematicienii au încetat în mare parte să mai încerce să demonstreze cel de-al cincilea postulat pornind de la celelalte patru postulate. În schimb, mulți matematicieni au început să studieze alte geometrii care nu respectă cel de-al cincilea postulat al lui Euclid.
O altă axiomă cu care matematicienii înlocuiesc uneori a cincea axiomă a lui Euclid spune că:
Dată fiind o dreaptă și un punct care nu se află pe această dreaptă, puteți trasa cel puțin două drepte care trec prin acest punct și care, în cele din urmă, nu se vor intersecta cu cealaltă dreaptă.
Aceasta se numește geometrie hiperbolică.
O altă geometrie elimină pur și simplu cel de-al cincilea postulat al lui Euclid și nu îl înlocuiește cu nimic. Aceasta se numește geometrie neutră sau geometrie absolută.
Căuta în