Forma universului
Forma Universului nu poate fi discutată în termeni obișnuiți, deoarece toți termenii trebuie să fie cei ai relativității einsteiniene. Prin urmare, geometria universului nu este geometria euclidiană obișnuită din viața noastră de zi cu zi.
Conform teoriei speciale a relativității, este imposibil de spus dacă două evenimente distincte au loc în același timp dacă aceste evenimente sunt separate în spațiu. A vorbi despre "forma universului (la un moment dat)" este naiv din punctul de vedere al relativității restrânse. Din cauza relativității simultaneității, nu putem vorbi despre puncte diferite din spațiu ca fiind "în același moment în timp" și, prin urmare, nici despre "forma universului la un moment dat".
Ceea ce fac astrofizicienii este să se întrebe dacă un anumit model al universului este compatibil cu ceea ce se cunoaște prin observații și măsurători ale universului. Dacă universul observabil este mai mic decât întregul univers (în unele modele este cu multe ordine de mărime mai mic sau chiar infinitezimal), observația este limitată la o parte a întregului.
Considerațiile privind forma universului pot fi împărțite în două:
- geometria locală, care se referă în special la curbura universului, mai ales în universul observabil, și
- geometria globală, care se referă la topologia universului ca întreg, a cărei măsurare poate fi imposibilă.
Universul observabil este baza pentru testarea oricărui model al universului. Acesta este un volum sferic (o minge) centrat pe observator, indiferent de forma universului în ansamblu. Fiecare locație din univers are propriul univers observabil, care se poate suprapune sau nu cu cel centrat pe Pământ.
Măsurătorile recente au determinat NASA să declare: "Acum știm că universul este plat cu o marjă de eroare de numai 0,4%". În cadrul unui model, modelul FLRW, cea mai populară formă a Universului care se potrivește cu datele observaționale este modelul plat infinit. Există și alte modele care se potrivesc datelor.
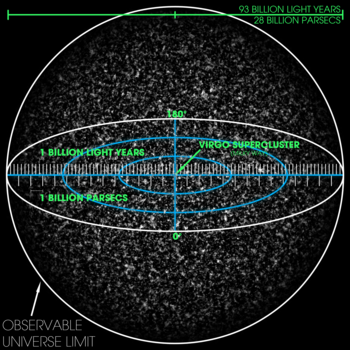
Vizualizare tridimensională a universului observabil de 93 de miliarde de ani lumină - sau 28 de miliarde de parsecuri. Scara este de așa natură încât granulele fine reprezintă colecții de un număr mare de superclustere. Superclusterul Virgo - casa Căii Lactee - este marcat în centru, dar este prea mic pentru a fi văzut în imagine.
Întrebări și răspunsuri
Î: Care este forma universului conform observațiilor actuale?
R: Conform măsurătorilor recente, NASA a declarat că universul este plat, cu o marjă de eroare de numai 0,4%.
Î: Cum afectează relativitatea specială înțelegerea noastră cu privire la forma universului?
R: Din cauza relativității simultaneității, este imposibil să se spună dacă două evenimente distincte au loc în același timp dacă aceste evenimente sunt separate în spațiu. Aceasta înseamnă că nu putem vorbi despre puncte diferite din spațiu ca fiind "în același moment în timp" și, prin urmare, nici despre "forma universului la un moment dat".
Î: Ce tip de geometrie folosesc astrofizicienii atunci când discută despre forma Universului?
R: Astrofizicienii folosesc relativitatea einsteiniană atunci când discută și testează modelele de descriere și predicție a unor aspecte legate de Univers. Ei iau în considerare, de asemenea, geometria locală, care se referă în special la curbură, și geometria globală, care se referă la topologie.
Î: Fiecare locație din Univers face parte dintr-un univers observabil?
R: Da, fiecare locație din Univers are propriul său univers observabil, care se poate suprapune sau nu cu cel centrat pe Pământ.
Î: Ce se înțelege prin "plat" atunci când ne referim la un model de descriere/predicție a unor aspecte legate de Univers?
R: În cadrul unui model, numit FLRW (Friedmann-Lemaître-Robertson-Walker), "plat" se referă la un model plat infinit care se potrivește cel mai bine datelor observaționale. Înseamnă că spațiul pare uniform, indiferent de locul în care te uiți și că nu există curbe sau curburi prezente în cadrul acestui model particular.
Î: Există și alte modele care se potrivesc datelor observaționale în afară de modelul plat infinit al lui FLRW?
R: Da, există și alte modele care se potrivesc cu datele observaționale în afară de modelul plat infinit al lui FLRW.
