Moment magnetic

Două definiții ale momentului

În manualele de specialitate, se folosesc două abordări complementare pentru a defini momentele magnetice. În manualele de dinainte de 1930, acestea erau definite cu ajutorul polilor magnetici. Cele mai recente manuale le definesc în termeni de curenți Ampèrian.

Definiția polului magnetic

Fizicienii reprezintă sursele de momente magnetice din materiale sub forma unor poli. Polii Nord și Sud sunt o analogie cu sarcinile pozitive și negative din electrostatică. Luați în considerare o bară magnetică care are poli magnetici de magnitudine egală, dar de polaritate opusă. Fiecare pol este sursa forței magnetice care slăbește odată cu distanța. Deoarece polii magnetici vin întotdeauna în perechi, forțele lor se anulează parțial, deoarece în timp ce un pol trage, celălalt respinge. Această anulare este mai mare atunci când polii sunt apropiați unul de celălalt, adică atunci când bara magnetică este scurtă. Prin urmare, forța magnetică produsă de o bară magnetică, într-un anumit punct din spațiu, depinde de doi factori: atât de puterea p {\displaystyle p} a polilor săi, cât și de vectorul l {\displaystyle \mathbf {l}. } care îi separă. Momentul se definește astfel

m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . }

Acesta indică direcția de la polul sud la polul nord. Analogia cu dipolii electrici nu trebuie dusă prea departe, deoarece dipolii magnetici sunt asociați cu momentul unghiular (a se vedea Moment magnetic și moment unghiular). Cu toate acestea, polii magnetici sunt foarte utili pentru calculele magnetostatice, în special în aplicațiile la feromagneți. Practicienii care utilizează abordarea polilor magnetici reprezintă în general câmpul magnetic prin câmpul ireotațional H {\displaystyle \mathbf {H} } , prin analogie cu câmpul electric E {\displaystyle \mathbf {E}. } .

Definiția buclei de curent

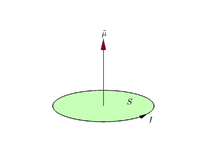
Să presupunem că o buclă plană închisă transportă un curent electric I {\displaystyle I} și are aria vectorială S {\displaystyle \mathbf {S}. } ( x {\displaystyle x} , y {\displaystyle y} și coordonatele z {\displaystyle z} ale acestui vector sunt ariile proiecțiilor buclei pe y z {\displaystyle yz}. , z x {\displaystyle zx} și x y {\displaystyle xy}). Momentul său magnetic m {\displaystyle \mathbf {m} } , vector, se definește astfel:

m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . }

Prin convenție, direcția suprafeței vectoriale este dată de regula strângerii mâinii drepte (îndoirea degetelor mâinii drepte în direcția curentului în jurul buclei, când palma mâinii "atinge" marginea exterioară a buclei, iar degetul mare drept indică direcția suprafeței vectoriale și, prin urmare, a momentului magnetic).

În cazul în care bucla nu este plană, momentul este dat de formula

m = I 2∫ r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}}\int \mathbf {r} \times {\rm {d}\mathbf {r} . }

În cazul cel mai general al unei distribuții arbitrare de curent în spațiu, momentul magnetic al unei astfel de distribuții poate fi găsit din următoarea ecuație:

m = 12∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,}

unde r {\displaystyle \mathbf {r} } este vectorul de poziție îndreptat de la origine către locația elementului de volum, iar J {\displaystyle \mathbf {J} } este vectorul de densitate a curentului în locația respectivă.

Ecuația de mai sus poate fi utilizată pentru a calcula momentul magnetic al oricărui ansamblu de sarcini în mișcare, cum ar fi un solid încărcat în rotație, înlocuind

J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,}

unde ρ {\displaystyle \rho } este densitatea de sarcină electrică într-un anumit punct, iar v {\displaystyle \mathbf {v} } este viteza liniară instantanee a acelui punct.

De exemplu, momentul magnetic produs de o sarcină electrică care se deplasează pe o traiectorie circulară este

m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\,\mathbf {r} \times \mathbf {v} } ,

unde r {\displaystyle \mathbf {r} } este poziția încărcăturii q {\displaystyle q} în raport cu centrul cercului, iar v {\displaystyle \mathbf {v} } este viteza instantanee a încărcăturii.

Practicienii care folosesc modelul buclei de curent reprezintă în general câmpul magnetic prin câmpul solenoidal B {\displaystyle \mathbf {B} } analog cu câmpul electrostatic D {\displaystyle \mathbf {D} } .

Momentul magnetic al unui solenoid

O generalizare a buclei de curent de mai sus este o bobină cu mai multe ture sau un solenoid. Momentul său este suma vectorială a momentelor momentelor fiecărei spire în parte. În cazul în care solenoidul are N {\displaystyle N} spire identice (înfășurare cu un singur strat),

m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . }

Imagine 3D a unui solenoid.


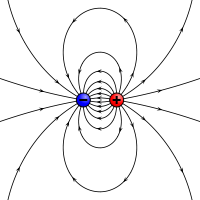
Un analog electrostatic pentru un moment magnetic: două sarcini opuse separate de o distanță finită.

Unități

Unitatea pentru momentul magnetic nu este o unitate de bază în Sistemul Internațional de Unități (SI) și poate fi reprezentată în mai multe moduri. De exemplu, în definiția buclei de curent, suprafața se măsoară în metri pătrați, iar I {\displaystyle I} se măsoară în amperi, astfel încât momentul magnetic se măsoară în amperi-metri pătrați ( A m {\displaystyle2 {\text{A m}}^{2}}} ). În ecuația pentru cuplul asupra unui moment, cuplul este măsurat în Newton.metri, iar câmpul magnetic în tesla, astfel încât momentul este măsurat în N.m pe Tesla ( N.m T - 1{\displaystyle {\text{N.m T}}^{-1}} ). Aceste două reprezentări sunt echivalente:

A m = 2N.m T -1 . {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. }

În sistemul CGS, există mai multe seturi diferite de unități de electromagnetism, dintre care cele principale sunt ESU, Gaussian și EMU. Dintre acestea, există două unități alternative (neechivalente) de moment de dipol magnetic în CGS:

(ESU CGS) 1 statA-cm² = 3.33564095×10^-14 (m-A² sau N.m/T)

și (mai frecvent utilizate)

(EMU CGS și Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10^-3 (m-A² sau N.m/T).

Raportul dintre aceste două unități CGS neechivalente (EMU/ESU) este exact egal cu viteza luminii în spațiul liber, exprimată în cm/s.

Toate formulele din acest articol sunt corecte în unități SI, dar în alte sisteme de unități, este posibil ca formulele să trebuiască să fie modificate. De exemplu, în unitățile SI, o buclă de curent cu curentul I și suprafața A are momentul magnetic I×A (a se vedea mai jos), dar în unitățile gaussiene momentul magnetic este I×A/c.

Momente magnetice intrinseci și spini ai unor particule elementare
Particule	Momentul de dipol magnetic în unități SI (10 −27J/T)	Numărul cuantic de spin (adimensional)
electron	-9284.764	1/2
proton	14.106067	1/2
neutron	-9.66236	1/2
muon	-44.904478	1/2
deuteron	4.3307346	1
triton	15.046094	1/2

Pentru relația dintre noțiunile de moment magnetic și magnetizare, a se vedea magnetizare.