Formula lui Euler | ecuație care implică numere complexe și funcții trigonometrice

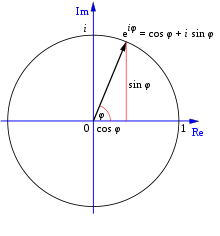
În analiza complexă, formula lui Euler, denumită uneori și relația lui Euler, este o ecuație care implică numere complexe și funcții trigonometrice. Mai exact, aceasta afirmă că

e i x = cos x + i sin x {\displaystyle e^{ix}=\cos x+i\sin x} $e^{ix}=\cos x+i\sin x$

unde x este un număr real, e este numărul lui Euler și i este unitatea imaginară.

Se face o relație între funcțiile trigonometrice și funcțiile exponențiale ale numerelor complexe. Este denumită după Leonhard Euler, care a publicat-o în 1748. Când a publicat-o, Euler a spus că unghiul trebuie să fie un număr real. Ulterior, s-a dovedit că formula funcționează și dacă unghiul nu este un număr real, ci unul complex.

Atunci când unghiul este π {\displaystyle \pi } $\pi$ și 2 π {\displaystyle 2\pi } $2\pi$ , formula lui Euler devine e i π = - 1 {\displaystyle e^{i\pi }=-1} $e^{i\pi }=-1$ și e i 2 π = 1 {\displaystyle e^{i2\pi }=1}. $e^{i2\pi }=1$ , respectiv.

Pagini conexe

Identitatea lui Euler

Întrebări și răspunsuri

Î: Ce este formula lui Euler?

R: Formula lui Euler este o ecuație care implică numere complexe și funcții trigonometrice și care leagă funcțiile exponențiale ale numerelor complexe de funcțiile trigonometrice.

Î: Cine a publicat formula lui Euler?

R: Leonhard Euler a publicat formula lui Euler în 1748.

Î: Funcționează formula atunci când unghiul nu este un număr real?

R: Da, se pare că formula funcționează și în cazul în care unghiul este un număr complex.

Î: Ce se întâmplă atunci când unghiul este pi?

R: Atunci când unghiul este pi, formula lui Euler devine e^iנ = -1.

Î: Ce se întâmplă când unghiul este 2pi?

R: Când unghiul este 2pi, formula lui Euler devine e^i2נ = 1.

Î: Ce reprezintă "e" în această ecuație?

R: În această ecuație, "e" reprezintă numărul lui Euler.

Î: Ce reprezintă "i" în această ecuație?

R: În această ecuație, "i" reprezintă unitatea imaginară.