Funcția exponențială e^x — definiție, proprietăți și aplicații

În matematică, funcția exponențială este o funcție care crește din ce în ce mai repede. Mai exact, este funcția exp ( x ) = e x {\displaystyle \exp(x)=e^{x}}. {\displaystyle \exp(x)=e^{x}}, unde e este constanta lui Euler, un număr irațional care este aproximativ 2,71828.


 

Definiții echivalente

  • Definiție prin serie: exp(x) se definește prin seria Σ_{k=0}^{∞} x^k / k!, adică exp(x) = 1 + x + x^2/2! + x^3/3! + … . Această serie converge pentru orice x ∈ ℝ (și, de fapt, pentru orice x ∈ ℂ).
  • Definiție prin limită: exp(x) = lim_{n→∞} (1 + x/n)^n.
  • Definiție funcțională: exp(x+y) = exp(x)·exp(y) și exp′(0) = 1; aceste proprietăți determină funcția exponențială în mod unic.

Proprietăți de bază

  • Domain: toți numerele reale, adică ℝ. Range: (0, ∞) — exp(x) este întotdeauna pozitivă și niciodată zero.
  • Monotonie: exp(x) este strict crescătoare pe ℝ.
  • Convexitate: exp(x) este strict convexă pe ℝ.
  • Identități importante:
    • exp(0) = 1
    • exp(x+y) = exp(x)·exp(y)
    • exp(-x) = 1/exp(x)
    • exp(nx) = (exp(x))^n pentru orice întreg n
  • Limite: lim_{x→-∞} exp(x) = 0 și lim_{x→+∞} exp(x) = +∞.

Derivate și integrale

  • Derivata: d/dx exp(x) = exp(x). Funcția este singura (peste funcțiile suficient de regulate) care este egală cu propria derivată.
  • Integrală: ∫ exp(x) dx = exp(x) + C.
  • Mai general, pentru constante a,b: d/dx exp(ax+b) = a·exp(ax+b), iar ∫ exp(ax+b) dx = (1/a) exp(ax+b) + C (pentru a ≠ 0).

Suma în serie și convergența

Seria Taylor centrată în 0 este exp(x) = Σ_{k=0}^∞ x^k/k!, care converge uniform pe orice interval compact și definește o funcție entire (adică derivabilă analitic pe toată linia complexă).

Logaritmul invers și ecuații exponentiale

  • Funcția inversă a exp este logaritmul natural ln: dacă y = exp(x) atunci x = ln(y). Domainul ln este (0, ∞).
  • Pentru rezolvarea ecuațiilor de forma exp(x) = a (a>0) avem x = ln(a).
  • Generalizare: pentru orice bază a>0, a ≠ 1, a^x = exp(x·ln a).

Extinderea la numere complexe

Pe ℂ, exp(z) este definită prin aceeași serie și are proprietăți similare. Un rezultat fundamental este formula lui Euler: exp(iθ) = cos θ + i sin θ, care leagă exponentiala complexă de funcțiile trigonometrice.

Aplicații

  • Modelare a creșterii/exponențiale: procese ca populația într-un model fără resurse limitate sau dobânda compusă continuu: A(t)=A₀ exp(rt).
  • Ecuatii diferențiale: soluțiile ecuațiilor liniare cu coeficienți constanți apar frecvent ca exp(kt). Exemplu: dy/dt = k y ⇒ y(t) = y(0) exp(kt).
  • Decădere radioactivă: N(t) = N₀ exp(-λ t); timpul de înjumătățire t_{1/2} = ln 2 / λ.
  • Finanțe: dobânda compusă continuu: A = P exp(rt) (limită a dobânzii compuse pe perioade n → ∞).
  • Analiză complexă și fizică: modularea undelor, transformata Laplace/Fourier, ecuațiile de evoluție liniare și multe formule din fizică (de ex. distribuții statistice, funcții de transfer).

Exemple numerice și observații practice

  • Valori: exp(1) ≈ 2,718281828…, exp(2) ≈ 7,389056…, exp(-1) ≈ 0,367879…
  • Pentru calcul numeric se folosesc funcții dedicate (de ex. exp în bibliotecile de calcul), iar seria Taylor sau metodele algoritmice rapide permit evaluarea foarte precisă pentru orice x.

Scurtă recapitulare

Funcția exponențială exp(x) = e^x este o funcție definitorie în analiză și aplicații: este pozitivă, monotonic crescătoare, egală cu propria derivată, are seria Taylor convergentă pe toată axa reală și apare în mod natural în modele de creștere/decădere, în soluții de ecuații diferențiale și în analiza complexă.

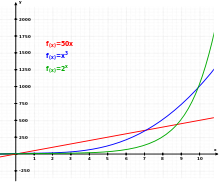
Trei funcții diferite: Lineară (roșu), Cubică (albastru) și Exponențială (verde).  Zoom
Trei funcții diferite: Lineară (roșu), Cubică (albastru) și Exponențială (verde).  

Proprietăți

Deoarece funcțiile exponențiale utilizează exponențializarea, acestea urmează aceleași reguli de exponenți. Astfel,

e x + y = exp ( x + y ) = exp ( x ) exp ( y ) = e x e y {\displaystyle e^{x+y}=\exp(x+y)=\exp(x)\exp(y)=e^{x}e^{y}}} {\displaystyle e^{x+y}=\exp(x+y)=\exp(x)\exp(y)=e^{x}e^{y}}.

Aceasta urmează regula că x a ⋅ x b = x a + b {\displaystyle x^{a}\cdot x^{b}=x^{a+b}}. {\displaystyle x^{a}\cdot x^{b}=x^{a+b}}.

Logaritmul natural este operația inversă a unei funcții exponențiale, unde:

ln ( x ) = log e ( x ) = log ( x ) log ( e ) {\displaystyle \lnn(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}}}{\frac {\log(e)}}} {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}}

Funcția exponențială satisface o proprietate interesantă și importantă în calculul diferențial:

d d d x e x e x = e x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}}

Acest lucru înseamnă că panta funcției exponențiale este însăși funcția exponențială și, ca urmare, are o pantă de 1 la x = 0 {\displaystyle x=0}{\displaystyle x=0} . Aceste proprietăți sunt motivul pentru care este o funcție importantă în matematică.



 

Aplicații

Funcția exponențială generală, în care baza nu este neapărat e {\displaystyle e} {\displaystyle e}, este una dintre cele mai utile funcții matematice. Este utilizată pentru a reprezenta creșterea exponențială, care are utilizări în aproape toate disciplinele științifice și este, de asemenea, importantă în domeniul financiar. O altă aplicație a funcției exponențiale este descreșterea exponențială, care apare în cazul descompunerii radioactive și al absorbției luminii.

Un exemplu de funcție exponențială în viața reală ar fi dobânda la o bancă. Dacă o persoană depune 100 de lire sterline într-un cont care primește o dobândă de 3% pe lună, atunci soldul din fiecare lună (presupunând că banii sunt neatinși) ar fi următorul:

Luna

Balanță

Luna

Balanță

Ianuarie

£100.00

Iulie

£119.41

Februarie

£103.00

August

£122.99

Martie

£106.09

Septembrie

£126.68

Aprilie

£109.27

Octombrie

£130.48

Mai

£112.55

Noiembrie

£134.39

Iunie

£115.93

Decembrie

£138.42

Aici, observați cum banii în plus din dobândă cresc în fiecare lună, în sensul că, cu cât soldul inițial este mai mare, cu atât mai multă dobândă va primi persoana respectivă.

Două exemple matematice de funcții exponențiale (cu baza a) sunt prezentate mai jos.

a=2

x {\displaystyle x} x

Rezultat

-2

0.25

-1

0.5

0

1

1

2

2

4

3

8

4

16

a=3

x {\displaystyle x} x

Rezultat

-2

1/ 9

-1

1/ 3

0

1

1

3

2

9

3

27

4

81


 

Relația cu constanta matematică e

Chiar dacă baza ( a {\displaystyle a}a ) poate fi orice număr mai mare decât zero, de exemplu, 10 sau 1/2, adesea este un număr special numit e. Numărul e nu poate fi scris cu exactitate, dar este aproape egal cu 2,71828.

Numărul e este important pentru fiecare funcție exponențială. De exemplu, o bancă plătește o dobândă de 0,01% în fiecare zi. O persoană își ia banii de dobândă și îi pune într-o cutie. După 10.000 de zile (aproximativ 30 de ani), are de 2 ori mai mulți bani decât la început. O altă persoană își ia banii cu dobândă și îi pune înapoi în bancă. Deoarece banca îi plătește acum dobândă pentru dobânda sa, suma de bani este o funcție exponențială.

De fapt, după 10.000 de zile, el nu are de 2 ori mai mulți bani decât la început, ci de 2,718145 ori mai mulți bani decât la început. Acest număr este foarte apropiat de numărul e. Dacă banca plătește dobânda mai des, astfel încât suma plătită de fiecare dată să fie mai mică, atunci numărul va fi mai apropiat de numărul e.

O persoană poate, de asemenea, să se uite la imagine pentru a vedea de ce numărul e este important pentru funcțiile exponențiale. Imaginea are trei curbe diferite. Curba cu puncte negre este o funcție exponențială cu o bază ușor mai mică decât e. Curba cu linii negre scurte este o funcție exponențială cu o bază ușor mai mare decât e. Curba albastră este o funcție exponențială cu o bază exact egală cu e. Linia roșie este tangentă la curba albastră. Ea atinge curba albastră într-un punct fără a o intersecta. O persoană poate vedea că curba roșie traversează axa x, linia care merge de la stânga la dreapta la -1. Acest lucru este valabil numai pentru curba albastră. Acesta este motivul pentru care funcția exponențială cu baza e este specială.



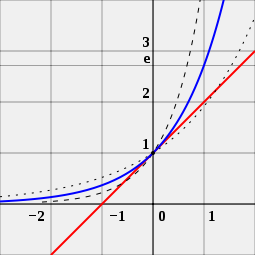
 e este unicul număr a, astfel încât valoarea derivatei funcției exponențiale f (x) = ax (curba albastră) în punctul x = 0 să fie exact 1. Pentru comparație, sunt prezentate funcțiile 2x (curba punctată) și 4x (curba punctată); acestea nu sunt tangente la dreapta cu panta 1 (roșie).  Zoom
e este unicul număr a, astfel încât valoarea derivatei funcției exponențiale f (x) = ax (curba albastră) în punctul x = 0 să fie exact 1. Pentru comparație, sunt prezentate funcțiile 2x (curba punctată) și 4x (curba punctată); acestea nu sunt tangente la dreapta cu panta 1 (roșie).  

Pagini conexe



 

Întrebări și răspunsuri

Î: Ce este funcția exponențială?


R: Funcția exponențială este o funcție matematică care crește din ce în ce mai repede.

Î: Cum se exprimă matematic funcția exponențială?


R: Funcția exponențială se exprimă matematic sub forma exp(x) = e^x, unde e este constanta lui Euler.

Î: Ce reprezintă constanta lui Euler?


R: Constanta lui Euler reprezintă un număr irațional care este aproximativ 2,71828.

Î: Funcția exponențială este întotdeauna crescătoare?


R: Da, funcția exponențială crește întotdeauna ca valoare pe măsură ce x crește.

Î: Există vreo limită la cât de repede poate crește funcția exponențială?


R: Nu, nu există o limită a vitezei cu care poate crește funcția exponențială, deoarece aceasta continuă să crească cu valori mai mari ale lui x.

Î: Cum putem calcula constanta lui Euler?


R: Putem calcula constanta lui Euler utilizând metode numerice, cum ar fi seriile Taylor sau fracțiile continue.

Î: Ce alte aplicații are funcția exponențială în afară de matematică?


R: Funcția exponențială are multe aplicații în afara matematicii, inclusiv în fizică, chimie, biologie, economie și inginerie.

AlegsaOnline.com - 2020 / 2025 - License CC3