Calcul diferențial | studiul de a afla rata de variație a unei variabile

Calculul diferențial, o ramură a calculului, este studiul care constă în aflarea ratei de variație a unei variabile în comparație cu o altă variabilă, prin utilizarea funcțiilor. Este o modalitate de a afla cum se schimbă o formă dintr-un punct în altul, fără a fi nevoie să împărțim forma într-un număr infinit de bucăți. Calculul diferențial este opusul calculului integral. Acesta a fost dezvoltat în anii 1670 și 1680 de Sir Isaac Newton și Gottfried Leibniz.

Fond

Spre deosebire de un număr precum 5 sau 200, o variabilă își poate schimba valoarea. De exemplu, distanța și timpul sunt variabile. La o cursă olimpică de alergare, pe măsură ce o persoană aleargă, distanța de la linia de start crește. Între timp, un cronometru sau un ceas măsoară timpul pe măsură ce acesta crește. Putem măsura viteza medie a alergătorului, dacă împărțim distanța parcursă de acesta la timpul necesar. Dar acest lucru nu ne spune cu ce viteză alerga persoana respectivă exact la 1,5 secunde după începerea cursei. Dacă am avea distanța la 1 secundă și distanța la 2 secunde, am avea în continuare doar o medie, deși aceasta ar fi probabil mai corectă decât media pentru întreaga cursă.

Până la inventarea calculului, singura modalitate de a afla acest lucru era să tăiem timpul în bucăți din ce în ce mai mici, astfel încât viteza medie pe parcursul timpului mai mic să se apropie din ce în ce mai mult de viteza reală la exact 1,5 secunde. Acesta era un proces foarte lung și dificil și trebuia făcut de fiecare dată când oamenii doreau să rezolve ceva. Cu siguranță, este mult mai dificil pentru un șofer să își dea seama de viteza unei mașini folosind doar odometrul (contorul de distanță) și ceasul - fără un vitezometru.

O problemă foarte asemănătoare este aceea de a găsi panta (cât de abruptă este) în orice punct al unei curbe. Panta unei linii drepte este ușor de calculat - este pur și simplu cât de mult urcă (y sau verticală) împărțită la cât de mult traversează (x sau orizontală). Dacă o dreaptă este paralelă cu axa x, atunci panta ei este zero. Dacă o linie dreaptă a trecut prin (x,y) = (2,10) și (4,18), linia urcă 8 și traversează 2, deci panta ei este 8 împărțit la 2, ceea ce înseamnă 4.

Pe o "curbă", însă, panta este variabilă (are valori diferite în puncte diferite), deoarece linia se îndoaie. Dar dacă curba ar fi tăiată în bucăți foarte, foarte mici, curba în acel punct ar arăta aproape ca o linie dreaptă foarte scurtă. Astfel, pentru a calcula panta acesteia, se poate trasa o linie dreaptă care să treacă prin punct cu aceeași pantă ca și curba din acel punct. Dacă se face exact cum trebuie, linia dreaptă va avea aceeași pantă ca și curba și se numește tangentă. Dar nu există nicio modalitate de a ști (fără calcul) dacă tangenta este exact corectă, iar ochii noștri nu sunt suficient de preciși pentru a fi siguri dacă este exactă sau pur și simplu foarte apropiată.

Newton și Leibniz au găsit o modalitate de a calcula exact panta (sau viteza în exemplul distanței), folosind reguli simple și logice. Ei au împărțit curba într-un număr infinit de bucăți foarte mici. Apoi au ales puncte de o parte și de alta a punctului care îi interesa și au calculat tangentele la fiecare dintre ele. Pe măsură ce punctele se apropiau unele de altele spre punctul care îi interesa, panta se apropia de o anumită valoare, pe măsură ce tangentele se apropiau de panta reală a curbei. Ei au spus că această valoare specială de care se apropia era panta reală.

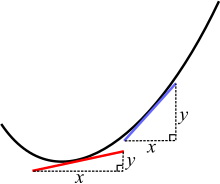
Pe o curbă, două puncte diferite au pante diferite. Liniile roșie și albastră sunt tangente la curbă.

Cum funcționează

Să spunem că avem o funcție y = f(x). f este prescurtarea de la funcția, deci această ecuație înseamnă "y este o funcție de x". Acest lucru ne spune că înălțimea lui y pe axa verticală depinde de valoarea lui x (axa orizontală) în acel moment. De exemplu, cu ecuația y = x², știm că dacă x este 1, atunci y va fi 1; dacă x este 3, atunci y va fi 9; dacă x este 20, atunci y va fi 400.

Alegeți un punct A de pe curbă și numiți poziția sa orizontală x. Apoi alegeți un alt punct B de pe curbă, care este puțin mai îndepărtat decât A, și numiți poziția sa orizontală x + h. Nu contează cât este h; este un număr foarte mic.

Deci, când mergem din punctul A în punctul B, poziția verticală a trecut de la f(x) la f(x + h), iar poziția orizontală a trecut de la x la x + h. Acum, amintiți-vă că panta reprezintă cât de mult urcă împărțită la cât de mult traversează. Așadar, panta va fi:

f ( x + h ) - f ( x ) h {\displaystyle {\frac {f(x+h)-f(x)}{h}}}} ${\frac {f(x+h)-f(x)}{h}}$

Dacă aducem B din ce în ce mai aproape de A - ceea ce înseamnă că h se apropie din ce în ce mai mult de 0 - atunci ne apropiem mai mult de a ști care este panta în punctul A.

lim h → 0 f ( x + h ) - f ( x ) h {\displaystyle \lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}}}} $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Acum să ne întoarcem la y = x². Panta acesteia poate fi determinată după cum urmează:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}{h}}end{aligned}}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

Aplicând teorema binomială, care afirmă în parte că ( x + y ) 2 = x 2 + 2 x y + y 2 {\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}}. $(x+y)^{2}=x^{2}+2xy+y^{2}$ , putem reduce expresia la:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}}{h}}\\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}{}}}2x\end{aligned}}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Deci știm, fără a fi nevoie să trasăm nicio tangentă, că în orice punct al curbei f(x) = x², derivata f'(x) (marcată cu apostrof) va fi 2x în orice punct. Acest proces de calcul al pantei cu ajutorul limitelor se numește diferențiere sau găsirea derivatei.

Leibniz a ajuns la același rezultat, dar a numit h "dx", ceea ce înseamnă "o cantitate infimă de x". El a numit schimbarea rezultată în f(x) "dy", ceea ce înseamnă "o cantitate mică de y". Notația lui Leibniz este folosită de mai multe cărți, deoarece este ușor de înțeles, atunci când ecuațiile devin mai complicate. În notația lui Leibniz:

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}}=f'(x)} ${\frac {dy}{dx}}=f'(x)$

O imagine care să arate ce înseamnă x și x + h pe curbă.

Reguli

Folosind sistemul de mai sus, matematicienii au elaborat reguli care funcționează tot timpul, indiferent de funcția analizată. (Notă: aici, u {\displaystyle u} $u$ și v {\displaystyle v} $v$ sunt ambele funcții de x {\displaystyle x} )

Stare	Funcția	Derivat	Exemplu	Derivat
Un număr în sine	y = a {\displaystyle y=a} $y=a$	d y d x = 0 {\displaystyle {\frac {dy}{dx}}=0}} ${\frac {dy}{dx}}=0$	y = 3 {\displaystyle y=3} $y=3$	0 {\displaystyle 0} $0$
O linie dreaptă	y = m x + c {\displaystyle y=mx+c} $y=mx+c$	d y d x = m {\displaystyle {\frac {dy}{dx}}=m} ${\frac {dy}{dx}}=m$	y = 3 x + 5 {\displaystyle y=3x+5} $y=3x+5$	3 {\displaystyle 3} $3$
x la puterea unui număr	x a {\displaystyle x^{a}} $x^{a}$	d y d x = a x a - 1 {\displaystyle {\frac {dy}{dx}}=ax^{a-1}}} ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {\displaystyle x^{12}} $x^{12}$	12 x 11 {\displaystyle 12x^{11}} $12x^{11}$
Un număr înmulțit cu o funcție	y = c ⋅ u {\displaystyle y=c\cdot u} $y=c\cdot u$	d y d x = c d u d x {\displaystyle {\frac {dy}{dx}}=c{\frac {du}{dx}}}} ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {\displaystyle 3(2x+1)} $3(2x+1)$
O funcție plus o altă funcție	y = u + v {\displaystyle y=u+v} $y=u+v$	d y d x = d u d x + d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {\displaystyle y=3x^{2}+{\sqrt {x}}}}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 2 x {\displaystyle 6x+{\frac {1}{2{\sqrt {x}}}}} $6x+{\frac {1}{2{\sqrt {x}}}}$
O funcție minus o altă funcție	y = u - v {\displaystyle y=u-v} $y=u-v$	d y d x = d u d x - d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}}-{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\sqrt {x}}}}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 2 x {\displaystyle 6x-{\frac {1}{2{\sqrt {x}}}}} $6x-{\frac {1}{2{\sqrt {x}}}}$
Regula produsului O funcție înmulțită cu o altă funcție	y = u ⋅ v {\displaystyle y=u\cdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}}v+u{\frac {dv}{dx}}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {\displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Regula coeficientului O funcție împărțită la o altă funcție	y = u v {\displaystyle y={\frac {u}{v}}}} $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {dy}{dx}}={\frac {{frac {\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {\displaystyle y={\frac {x^{2}+2}{x-1}}}} $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\displaystyle {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
Regula lanțului Se utilizează pentru funcții compuse	y = u ∘ v {\displaystyle y=u\circ v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}}\cdot {\frac {du}{dx}}}} ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {\displaystyle y={\sqrt {2x-1}}} $y={\sqrt {2x-1}}$	2 2 2 2 x - 1 = 1 2 2 x - 1 {\displaystyle {\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
O funcție exponențială	y = e x {\displaystyle {\frac {}{}}y=e^{x}} ${\frac {}{}}y=e^{x}$	d y d x = e x {\displaystyle {\frac {dy}{dx}}=e^{x}}} ${\frac {dy}{dx}}=e^{x}$	y = e x {\displaystyle {\frac {}{}}y=e^{x}} ${\frac {}{}}y=e^{x}$	e x {\displaystyle {\frac {}{}}e^{x}}} ${\frac {}{}}e^{x}$

Pagini conexe

Derivată (matematică)
Operator diferențial
Ecuație diferențială ordinară
Analiza matematică

Întrebări și răspunsuri

Î: Ce este calculul diferențial?

R: Calculul diferențial este o ramură a calculului care studiază rata de variație a unei variabile în comparație cu o altă variabilă, prin utilizarea funcțiilor.

Î: Cum funcționează?

R: Calculul diferențial ne permite să aflăm cum se modifică o formă dintr-un punct în altul fără a fi nevoie să împărțim forma într-un număr infinit de bucăți.

Î: Cine a dezvoltat calculul diferențial?

R: Calculul diferențial a fost dezvoltat în anii 1670 și 1680 de Sir Isaac Newton și Gottfried Leibniz.

Î: Ce este calculul integral?

R: Calculul integral este opusul calculului diferențial. Este utilizat pentru a afla ariile sub curbe și volumele solidelor cu suprafețe curbe.

Î: Când a fost dezvoltat calculul diferențial?