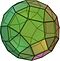
Solidul arhimedean

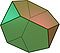
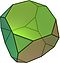
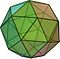
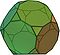
În geometrie, un solid arhimedean este o formă convexă compusă din poligoane. Este un poliedru, cu următoarele proprietăți:

Fiecare față este formată dintr-un poligon regulat
Toate colțurile formei arată la fel
Forma nu este nici un solid platonic, nici o prismă, nici o antiprismă.

În funcție de modul în care sunt numărate, există treisprezece sau cincisprezece astfel de forme. Din două dintre aceste forme, există două versiuni care nu pot fi făcute congruente prin rotație. Solidele arhimediene sunt denumite astfel după matematicianul grec antic Arhimede, care le-a descoperit probabil în secolul al III-lea î.Hr. Scrierile lui Arhimede s-au pierdut, dar Pappus din Alexandria le-a rezumat în secolul al IV-lea. În timpul Renașterii, artiștii și matematicienii au apreciat formele pure și au redescoperit toate aceste forme. Johannes Kepler a finalizat probabil această căutare în jurul anului 1620.

Pentru a construi un solid arhimedian este nevoie de cel puțin două poligoane diferite.

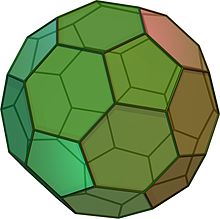
Un icosaedru trunchiat arată ca o minge de fotbal. Este alcătuit din 12 pentagoane echilaterale și 20 de hexagoane regulate. Are 60 de vârfuri și 90 de muchii. Este un solid arhimedian

Proprietăți

Solidele arhimediene sunt alcătuite din poligoane regulate, prin urmare toate marginile au aceeași lungime.
Toate solidele arhimediene pot fi produse din solide platonice, prin "tăierea marginilor" solidului platonic.
Tipul de poligoane care se întâlnesc într-un colț ("vertex") caracterizează atât solidul arhimedean, cât și pe cel platonic

Relația cu solidele platonice

Solidele platonice pot fi transformate în solide arhimediene, urmând o serie de reguli de construcție.

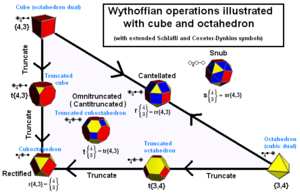
Solidele arhimediene pot fi construite ca poziții generatoare într-un caleidoscop

Lista de solide arhimediene

Următoarea este o listă a tuturor solidelor arhimediene

Imagine	Nume	Fețe	Tip	Marginile	Vertici
	Tetraedru trunchiat	8	4 triunghiuri 4 hexagoane	18	12
	Cuboctaedru	14	8 triunghiuri 6 pătrate	24	12
	Cub trunchiat	14	8 triunghiuri 6 octogoni	36	24
	Octaedru trunchiat	14	6 pătrate 8 hexagoane	36	24
	Rombicuboctaedru	26	8 triunghiuri 18 pătrate	48	24
	Cuboctaedru trunchiat	26	12 pătrate 8 hexagoane 6 octogoni	72	48
	Snub cube (2 versiuni oglindite)	38	32 de triunghiuri 6 pătrate	60	24
	Icosidodecaedru	32	20 de triunghiuri 12 pentagoni	60	30
	Dodecaedru trunchiat	32	20 de triunghiuri 12 decagoane	90	60
	Icozaedru trunchiat	32	12 pentagoni 20 de hexagoane	90	60
	Rombicosidodecaedru	62	20 triunghiuri30 pătrate12 pentagoni	120	60
	icosidodecaedru trunchiat	62	30 de pătrate 20 de hexagoane 12 decagoane	180	120
	Snub dodecaedru (2 versiuni oglindite)	92	80 de triunghiuri 12 pentagoni	150	60

Întrebări și răspunsuri

Î: Ce este un solid arhimedean?

R: Un solid arhimedean este o formă convexă formată din poligoane care are proprietățile ca fiecare față să fie un poligon regulat, toate colțurile să arate la fel și să nu fie un solid platonic, o prismă sau o antiprismă.

Î: Câte solide arhimediene există?

R: În funcție de modul în care sunt numărate, există fie treisprezece, fie cincisprezece solide arhimediene.

Î: Cine a descoperit solidele arhimediene?

R: Solidele arhimediene sunt denumite astfel după matematicianul grec antic Arhimede, care le-a descoperit probabil în secolul al III-lea î.Hr.

Î: Ce a făcut Pappus din Alexandria cu scrierile lui Arhimede?

R: Pappus din Alexandria a rezumat scrierile lui Arhimede despre solidele arhimediene în secolul al IV-lea.

Î: De ce au redescoperit artiștii și matematicienii solidele arhimediene în timpul Renașterii?

R: În timpul Renașterii, artiștii și matematicienii apreciau formele pure, iar solidele arhimediene erau considerate forme pure.

Î: Când a finalizat Johannes Kepler căutarea tuturor solidelor arhimediene?

R: Johannes Kepler a finalizat probabil căutarea tuturor solidelor arhimediene în jurul anului 1620.

Î: Ce este necesar pentru a construi un solid arhimedian?

R: Pentru a construi un solid arhimedean sunt necesare cel puțin două poligoane diferite.