Secțiunea de aur

Având un număr a și un alt număr mai mic b, raportul dintre cele două numere se găsește prin împărțirea lor. Raportul lor este a/b. Un alt raport se găsește prin adunarea celor două numere și împărțirea la numărul mai mare a. Noul raport este (a+b)/a. Dacă aceste două rapoarte sunt egale cu același număr, atunci acel număr se numește raport de aur. Litera greacă φ {\displaystyle \varphi } $\varphi$ (phi) este folosită de obicei ca denumire pentru raportul de aur.

De exemplu, dacă b = 1 și a/b = φ {\displaystyle \varphi } $\varphi$ , atunci a = φ {\displaystyle \varphi } $\varphi$ . Al doilea raport (a+b)/a este atunci ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } $(\varphi +1)/\varphi$ . Deoarece aceste două rapoarte sunt egale, acest lucru este adevărat:

φ = φ + 1 φ φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}} $\varphi ={\frac {\varphi +1}{\varphi }}$

Un mod de a scrie acest număr este

φ = 1 + 5 2 = 1.618... {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}=1.618...} $\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618...$

5 {\displaystyle {\sqrt {5}}} ${\sqrt {5}}$ este un număr care, atunci când este înmulțit cu el însuși, face 5: 5 × 5 = 5 {\displaystyle {\sqrt {5}}\times {\sqrt {5}}=5}} ${\sqrt {5}}\times {\sqrt {5}}=5$ .

Raportul de aur se numește număr irațional. Aceasta înseamnă că, dacă o persoană încearcă să îl scrie, nu se va opri niciodată și nu va forma niciodată un model, ci va începe astfel: 1.6180339887... Un lucru important în legătură cu acest număr este că, dacă scădeți 1 din el sau împărțiți 1 la el, veți obține același număr.

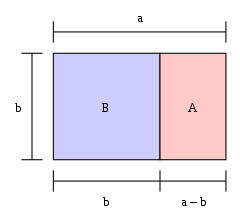
Dreptunghiul de aur

Dacă lungimea unui dreptunghi împărțită la lățimea sa este egală cu raportul de aur, atunci dreptunghiul este un "dreptunghi de aur". Dacă se taie un pătrat de la un capăt al unui dreptunghi de aur, atunci celălalt capăt este un nou dreptunghi de aur. În imagine, dreptunghiul mare (albastru și roz împreună) este un dreptunghi auriu, deoarece a / b = φ {\displaystyle a/b=\varphi } $a/b=\varphi$ . Partea albastră (B) este un pătrat, iar partea roz de una singură (A) este un alt dreptunghi auriu deoarece b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } $b/(a-b)=\varphi$ . Dreptunghiul mare și dreptunghiul roz au aceeași formă, dar dreptunghiul roz este mai mic și este întors.

Dreptunghiul mare BA este un dreptunghi auriu, adică proporția b:a este 1: φ {\displaystyle \varphi } $\varphi$ . Pentru orice astfel de dreptunghi, și numai pentru dreptunghiurile cu această proporție specifică, dacă eliminăm pătratul B, ceea ce rămâne, A, este un alt dreptunghi de aur; adică cu aceleași proporții ca și dreptunghiul inițial.

Numerele Fibonacci

Numerele lui Fibonacci sunt o listă de numere. O persoană poate găsi următorul număr din listă prin adăugarea ultimelor două numere împreună. Dacă o persoană împarte un număr din listă la numărul care l-a precedat, acest raport se apropie din ce în ce mai mult de raportul de aur.

Numărul Fibonacci	împărțită la cea anterioară	raport
1
1	1/1	= 1.0000
2	2/1	= 2.0000
3	3/2	= 1.5000
5	5/3	= 1.6667
8	8/5	= 1.6000
13	13/8	= 1.6250
21	21/13	= 1.6154...
34	34/21	= 1.6190...
55	55/34	= 1.6177...
89	89/55	= 1.6182...
...	...	...
	φ {\displaystyle \varphi } $\varphi$	= 1.6180...

Raportul de aur în natură

În natură, raportul de aur este adesea folosit pentru aranjarea frunzelor sau a florilor. Acestea folosesc unghiul de aur de aproximativ 137,5 grade. Frunzele sau florile dispuse în acest unghi folosesc cel mai bine lumina soarelui.

În plus, distanța dintre centrul corpului unei persoane și podea și distanța dintre creștetul capului și baza coloanei vertebrale sunt ambele în conformitate cu raportul de aur. În ciuda absenței sale din modelele comune de arhitectură și design, descoperirea lui Leonardo Fibonacci este recunoscută pe scară largă ca fiind revoluționară. Acesta poate lua forma uraganelor, a colților de elefant, a furnicilor, a ariciilor de mare, a stelelor de mare, a albinelor și a multor alte lucruri.

Secvența Fibonacci începe cu 0 și continuă la nesfârșit: 1, 1, 1, 2, 3, 3, 5, 8, 13, 21, 34, 55. Înainte de fiecare cifră există o sumă de două cifre. Modelul în sine este mai degrabă elementar și lipsit de importanță.

Asta până când afli că acest raport stă la baza frumuseții Mona Lisei, a membrelor umane, a criptării datelor și chiar a numărului de spirale de pe capul unei flori de floarea-soarelui. Se pare că universul are un mod natural de a ține evidența numerelor.

Florile au întotdeauna un număr impar de petale, în conformitate cu secvența Fibonacci. De exemplu, crinul păcii are trei petale, butucii au cinci, cicoarea are 21, margaretele au 34 și așa mai departe.

Iată alte câteva apariții naturale ale raportului de aur:

Capetele de semințe. Florile produc semințe în miezul lor, care apoi se răsucesc în spirală spre exterior pentru a umple capul florii.

Ananas, conopidă și broccoli Romanesco. În mod similar, acestea sunt conforme cu secvența Fibonacci.

Conuri de pin. Conurile de pin au modele spiralate pe păstăile de semințe, cu două spirale pe fiecare con care cresc în direcții opuse pe măsură ce cresc.

Ramuri de copac. În natură, acest model este observat atunci când un copac dezvoltă o ramură și apoi se împarte în două noi puncte de creștere. Apoi, doar una dintre cele două noi tulpini va crește în mod activ, în timp ce cealaltă va rămâne latentă.

Metode de zbor ale păsărilor. Cel mai bun unghi de atac al șoimului este perpendicular pe traiectoria de zbor a țintei, care este același cu pasul spiralei.

Galaxii spiralate. În Calea Lactee există mai multe brațe spiralate, fiecare cu o spirală logaritmică de aproximativ 12 grade.

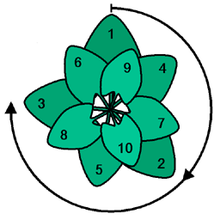
Utilizarea unghiului de aur va folosi în mod optim lumina soarelui. Aceasta este o vedere de sus.

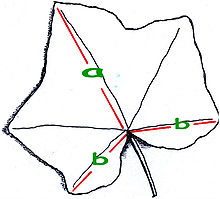
O frunză de iederă comună, care arată raportul de aur

Pagini conexe

Numerele Fibonacci
Phi

Întrebări și răspunsuri

Î: Care este raportul dintre două numere?

R: Raportul dintre două numere se găsește prin împărțirea lor, deci raportul ar fi a/b.

Î: Cum se poate găsi un alt raport?

R: Un alt raport poate fi găsit prin adunarea celor două numere și apoi împărțirea acestei sume la numărul mai mare, a. Acest nou raport ar fi (a+b)/a.

Î: Cum se numește situația în care aceste două rapoarte sunt egale între ele?

R: Atunci când aceste două rapoarte sunt egale între ele, se numește raportul de aur. Acesta este reprezentat de obicei cu litera greacă צ sau phi.

Î: Dacă b = 1 și a/b = צ , ce înseamnă asta pentru a?

R: Dacă b = 1 și a/b = צ , atunci înseamnă că și a = צ .

Î: Cum se poate scrie acest număr?

R: Un mod de a scrie acest număr este צ = 1 + 5 / 2 = 1,618...

Î: Ce înseamnă dacă scădem 1 din el sau împărțim 1 la el?

R: Dacă scădeți 1 din el sau împărțiți 1 la 1, veți obține înapoi același număr - cu alte cuvinte, ambele vor fi egale cu raportul de aur.

Î: Este rația de aur un număr irațional?

R: Da, rația de aur este un număr irațional, ceea ce înseamnă că, dacă cineva încearcă să o scrie, nu va exista niciodată un sfârșit și nici un model - doar începând cu ceva de genul "1,6180339887...".