Integrala de suprafață

Integrale de suprafață ale câmpurilor scalare

Se consideră o suprafață S pe care este definit un câmp scalar f. Dacă ne gândim la S ca fiind făcută dintr-un anumit material și pentru fiecare x din S numărul f(x) este densitatea materialului la x, atunci integrala de suprafață a lui f pe S este masa pe unitatea de grosime a lui S. (Acest lucru este adevărat numai dacă suprafața este o cochilie infinitezimală.) O abordare pentru calcularea integralei suprafeței este de a împărți suprafața în mai multe bucăți foarte mici, de a presupune că pe fiecare bucată densitatea este aproximativ constantă, de a găsi masa pe unitatea de grosime a fiecărei bucăți prin înmulțirea densității bucății cu aria acesteia și de a aduna numerele rezultate pentru a găsi masa totală pe unitatea de grosime a lui S.

Pentru a găsi o formulă explicită pentru integrala de suprafață, matematicienii parametrează S prin considerarea pe S a unui sistem de coordonate curbilinii, cum ar fi latitudinea și longitudinea pe o sferă. Fie ca o astfel de parametrizare să fie x(s, t), unde (s, t) variază într-o anumită regiune T din plan. Atunci, integrala suprafeței este dată de

∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \ peste \partial s}\times {\partial \mathbf {x} \peste \ partiala t}\ dreapta|ds\,dt}

unde expresia dintre barele din partea dreaptă este mărimea produsului încrucișat al derivatelor parțiale ale lui x(s, t).

De exemplu, pentru a afla suprafața unei forme funcționale generale, să z = f ( x , y ) {\displaystyle z=f\,(x,y)} , avem

A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \ peste \partial x}\times {\partial \mathbf {r} \ peste \partial y}\right\\|dx\,dy}

unde r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))} . Astfel încât ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))} , și ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))} . Deci,

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \ peste \partial x}\right)\times \left(0,1,{\partial f \ peste \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\||left(-{\partial f \ peste \partial x},-{\partial f \ peste \partial y},1\right)\right\||dx\,dy\\\&{}=\iint _{T}{\sqrt {\left({\partial f \ peste \partial x}\dreapta)^{2}+\left({\partial f \ peste \partial y}\dreapta)^{2}+1}}}\,\,dx\,dy\end{aligned}}}}

care este formula utilizată pentru suprafața unei forme funcționale generale. Vectorul din a doua linie de mai sus poate fi recunoscut ca fiind vectorul normal la suprafață.

Rețineți că, din cauza prezenței produsului încrucișat, formulele de mai sus funcționează numai pentru suprafețe încorporate în spațiul tridimensional.

Integrale de suprafață ale câmpurilor vectoriale

Se consideră un câmp vectorial v pe S, adică, pentru fiecare x din S, v(x) este un vector.

Integrala de suprafață poate fi definită în funcție de componente, în conformitate cu definiția integralei de suprafață a unui câmp scalar; rezultatul este un vector. De exemplu, acest lucru se aplică la câmpul electric într-un punct fix datorat unei suprafețe încărcate electric sau la gravitația într-un punct fix datorată unei foi de material. De asemenea, se poate calcula fluxul magnetic printr-o suprafață.

Alternativ, matematicienii pot integra componenta normală a câmpului vectorial; rezultatul este un scalar. Un exemplu este un fluid care curge prin S, astfel încât v(x) determină viteza fluidului la x. Fluxul este definit ca fiind cantitatea de fluid care curge prin S într-o unitate de timp.

Această ilustrație implică faptul că, dacă câmpul vectorial este tangent la S în fiecare punct, atunci fluxul este zero, deoarece fluidul curge doar în paralel cu S și nu intră și nici nu iese. Aceasta implică, de asemenea, că dacă v nu curge doar de-a lungul lui S, adică dacă v are atât o componentă tangențială, cât și una normală, atunci doar componenta normală contribuie la flux. Pe baza acestui raționament, pentru a găsi fluxul, trebuie să luăm produsul punctual al lui v cu suprafața unitară normală la S în fiecare punct, ceea ce ne va da un câmp scalar, și să integrăm câmpul obținut ca mai sus. Astfel se obține formula

∫ S S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s ∂ x ∂ x ∂ t ) d s d t . {\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \ peste \partial s}\times {\partial \mathbf {x} \ peste \partial t}\right)ds\,dt. }

Produsul încrucișat din partea dreaptă a acestei expresii este o normală de suprafață determinată de parametrizarea.

Această formulă definește integrala din stânga (a se observa punctul și notația vectorială pentru elementul de suprafață).

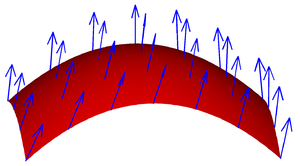
Un câmp vectorial pe o suprafață.

Teoreme care implică integrale de suprafață

Diferite rezultate utile pentru integralele de suprafață pot fi derivate folosind geometria diferențială și calculul vectorial, cum ar fi teorema divergenței și generalizarea acesteia, teorema lui Stokes.

Probleme avansate

Modificarea parametrizării

Discuția de mai sus a definit integrala de suprafață prin utilizarea unei parametrizări a suprafeței S. O anumită suprafață poate avea mai multe parametrizări. De exemplu, atunci când locațiile Polului Nord și Polului Sud sunt mutate pe o sferă, latitudinea și longitudinea se schimbă pentru toate punctele de pe sferă. O întrebare firească este dacă definiția integralei suprafeței depinde de parametrizarea aleasă. Pentru integralele câmpurilor scalare, răspunsul la această întrebare este simplu: valoarea integralei de suprafață va fi aceeași, indiferent de parametrizarea utilizată.

Integralele câmpurilor vectoriale sunt mai complicate, deoarece este implicată și normala la suprafață. Matematicienii au demonstrat că, în cazul a două parametrizări ale aceleiași suprafețe, ale căror normale de suprafață sunt îndreptate în aceeași direcție, ambele parametrizări dau aceeași valoare pentru integrala de suprafață. Cu toate acestea, în cazul în care normalele acestor parametrizări sunt orientate în direcții opuse, valoarea integralei de suprafață obținută cu ajutorul unei parametrizări este negativă față de cea obținută cu ajutorul celeilalte parametrizări. Rezultă că, având în vedere o suprafață, nu este necesar să ne rezumăm la o parametrizarea unică; dar, atunci când integrăm câmpuri vectoriale, trebuie să decidem în prealabil în ce direcție va fi orientată normala și apoi să alegem orice parametrizarea care corespunde acestei direcții.

Parametrizările funcționează pe părți ale suprafeței

O altă problemă este că uneori suprafețele nu au parametrizări care să acopere întreaga suprafață; acest lucru este valabil, de exemplu, pentru suprafața unui cilindru (de înălțime finită). Soluția evidentă este de a împărți suprafața respectivă în mai multe bucăți, de a calcula integrala suprafeței pe fiecare bucată și apoi de a le aduna pe toate. Acesta este într-adevăr modul în care funcționează lucrurile, dar atunci când se integrează câmpuri vectoriale trebuie să se fie din nou atenți la modul în care se alege vectorul de punctare a normalei pentru fiecare bucată de suprafață, astfel încât, atunci când bucățile sunt puse laolaltă, rezultatele să fie consecvente. În cazul cilindrului, aceasta înseamnă că, dacă decidem că pentru regiunea laterală normala va fi îndreptată în afara corpului, atunci pentru părțile circulare de sus și de jos, normala trebuie să fie îndreptată și ea în afara corpului.

Normale de suprafață inconsistente

În cele din urmă, există suprafețe care nu au o normală de suprafață în fiecare punct cu rezultate coerente (de exemplu, banda Möbius). Dacă o astfel de suprafață este împărțită în bucăți, pe fiecare bucată se alege o parametrizare și o normală de suprafață corespunzătoare, iar bucățile sunt puse din nou împreună, vectorii normali provenind din bucăți diferite nu pot fi reconcilianți. Acest lucru înseamnă că la o anumită joncțiune între două bucăți vor exista vectori normali îndreptați în direcții opuse. O astfel de suprafață se numește neorientabilă. Câmpurile vectoriale nu pot fi integrate pe suprafețe neorientabile.

Pagini conexe

• Teorema de divergență
• Teorema lui Stokes
• Integrala de linie
• Integrala de volum
• Sistem de coordonate carteziene
• Elemente de volum și de suprafață într-un sistem de coordonate sferice
• Elemente de volum și de suprafață într-un sistem de coordonate cilindrice
• Metoda Holstein-Herring