Serii armonice (matematică)

În matematică, seria armonică este o serie infinită divergentă:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Divergent înseamnă că, pe măsură ce adăugați mai mulți termeni, suma nu încetează să crească. Ea nu se îndreaptă spre o singură valoare finită.

Infinit înseamnă că puteți adăuga oricând un alt termen. Nu există un termen final al seriei.

Numele său provine de la ideea de armonice în muzică: lungimile de undă ale armonicilor unei coarde vibrante sunt 1/2,

1/3, 1/4, etc., din lungimea de undă fundamentală a coardei. În afară de primul termen, fiecare termen al seriei este media armonică a termenilor aflați de o parte și de alta a acestuia. Expresia "medie armonică" provine, de asemenea, din muzică.

Istorie

Faptul că seria armonică este divergentă a fost demonstrat pentru prima dată în secolul al XIV-lea de Nicole Oresme, dar a fost uitat. Dovezile au fost aduse în secolul al XVII-lea de Pietro Mengoli, Johann Bernoulli și Jacob Bernoulli.

Secvențele armonice au fost folosite de arhitecți. În perioada barocă, arhitecții le-au folosit în proporțiile planurilor, ale elevațiilor și în relațiile dintre detaliile arhitecturale ale bisericilor și palatelor.

Divergență

Există mai multe dovezi bine cunoscute ale divergenței seriei armonice. Câteva dintre ele sunt prezentate mai jos.

Test de comparație

O modalitate de a dovedi divergența este de a compara seria armonică cu o altă serie divergentă, în care fiecare numitor este înlocuit cu următoarea putere de doi mai mare:

1 + 1 2 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 6 + 1 7 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+{\cdots \\\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{{\color {red}{\mathbf {8}} }}}+{\frac {1}{{\color {roșu}{\mathbf {8} }}}+{\frac {1}{{\color {roșu}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {roșu}{\mathbf {16} }}}+\cdots \end{aligned}}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Fiecare termen al seriei armonice este mai mare sau egal cu termenul corespunzător al celei de-a doua serii și, prin urmare, suma seriei armonice trebuie să fie mai mare sau egală cu suma celei de-a doua serii. Cu toate acestea, suma celei de-a doua serii este infinită:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}}}\ +\!{\frac {1}{8}}}\ +\!{\frac {1}{8}}\dreapta)+\left({\frac {1}{16}}}\!+\!\cdots \!+\!{\frac {1}{16}}\dreapta)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\cdots =\infty \end{aligned}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Rezultă (prin testul de comparație) că suma seriilor armonice trebuie să fie și ea infinită. Mai precis, comparația de mai sus demonstrează că

∑ n = 1 2 k 1 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

pentru orice număr întreg pozitiv $k$ .

Această demonstrație, propusă de Nicole Oresme în jurul anului 1350, este considerată a fi un punct culminant al matematicii medievale. Ea este încă o demonstrație standard predată astăzi la cursurile de matematică.

Test integral

Este posibil să se demonstreze că seria armonică este divergentă prin compararea sumei sale cu o integrală improprie. Luați în considerare aranjamentul de dreptunghiuri prezentat în figura din dreapta. Fiecare dreptunghi are lățimea de 1 unitate și

1/n unități de înălțime, astfel încât suprafața totală a numărului infinit de dreptunghiuri este suma seriilor armonice:

aria dreptunghiurilor = 1 + 1 2 + 1 2 + 1 3 + 1 4 + 1 5 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area}\\\{text{rectunghiurilor}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Aria totală sub curba $y =$

1/x de la 1 la infinit este dată de o integrală improprie divergentă:

aria sub curbă = ∫ 1 ∞ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{zona de sub}}\\{{text{curbă}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}}\,dx=\infty .} ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Deoarece această suprafață este cuprinsă în întregime în dreptunghiuri, suprafața totală a dreptunghiurilor trebuie să fie și ea infinită. Acest lucru dovedește că

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).} $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Generalizarea acestui argument este cunoscută sub numele de testul integral.

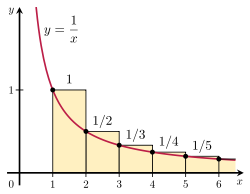
Ilustrație a testului integral.

Rata de divergență

Seria armonică diverge foarte lent. De exemplu, suma primilor 10 termeni⁴³ este mai mică de 100. Acest lucru se datorează faptului că sumele parțiale ale seriei au o creștere logaritmică. În special,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

unde $γ$ este constanta Euler-Mascheroni și $ε k ~$

1/2k, care se apropie de 0 pe măsură ce $k se apropie de$ infinit. Leonhard Euler a demonstrat atât acest lucru, cât și faptul că suma care include doar reciprocele numerelor prime este de asemenea divergentă, adică:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .} $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Sume parțiale

Primele treizeci de numere armonice
$n$	Suma parțială a seriei armonice, $H n$
$n$	exprimat ca fracțiune		zecimal	dimensiunea relativă
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Sumele parțiale finite ale seriilor armonice divergente,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

se numesc numere armonice.

Diferența dintre $H n$ și $ln n$ converge către constanta Euler-Mascheroni. Diferența dintre două numere armonice oarecare nu este niciodată un număr întreg. Niciun număr armonic nu este un număr întreg, cu excepția lui $H 1 = 1$ .

Serii conexe

Serii armonice alternative

Seria

∑ n = 1 ∞ ( - 1 ) n + 1 n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots } $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

este cunoscută sub numele de serie armonică alternantă. Această serie converge prin testul seriei alternante. În special, suma este egală cu logaritmul natural al lui 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

Seria armonică alternantă, deși convergentă condiționat, nu este absolut convergentă: dacă termenii din serie sunt rearanjate sistematic, în general suma devine diferită și, în funcție de rearanjare, poate fi chiar infinită.

Formula seriei armonice alternative este un caz special al seriei Mercator, seria Taylor pentru logaritmul natural.

O serie conexă poate fi derivată din seria Taylor pentru arctangenta:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.}. $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Aceasta este cunoscută sub numele de seria Leibniz.

Serii armonice generale

Seria armonică generală este de forma

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

unde $a \neq 0$ și $b$ sunt numere reale și

b/a nu este zero sau un număr întreg negativ.

Prin testul de comparare a limitelor cu seriile armonice, toate seriile armonice generale sunt, de asemenea, divergente.

$seria p$

O generalizare a seriei armonice este $seria p$ (sau seria hiperarmonică), definită ca fiind

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

pentru orice număr real $p.$ Când $p = 1$ , $seria p$ este seria armonică, care este divergentă. Fie testul integral, fie testul de condensare Cauchy arată că seria $p$ converge pentru orice $p > 1$ (caz în care se numește serie supraarmonică) și diverge pentru orice $p \leq 1$ . Dacă $p > 1$ , atunci suma $seriei p$ este ζ $(p)$ , adică funcția zeta Riemann evaluată la $p$ .

Problema găsirii sumei pentru $p = 2 se$ numește problema Basel; Leonhard Euler a arătat că este

$π$ ² /6. Valoarea sumei pentru $p = 3 se$ numește constanta lui Apéry, deoarece Roger Apéry a demonstrat că este un număr irațional.

ln-serie

În legătură cu seria $p$ este seria ln, definită ca fiind

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

pentru orice număr real pozitiv $p.$ Se poate demonstra, prin testul integral, că aceasta este divergentă pentru $p \leq 1,$ dar convergentă pentru toate $p > 1.$

$Seria φ$

Pentru orice funcție convexă, cu valori reale, $φ,$ astfel încât

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}}},} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

seria

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\dreapta)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

este convergentă.

Serii armonice aleatoare

Seria armonică aleatoare

∑ n = 1 ∞ s n n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}}{n}},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

unde $s n$ sunt variabile aleatoare independente, identic distribuite, care iau valorile +1 și -1 cu aceeași probabilitate

1/2, este un exemplu bine cunoscut în teoria probabilităților pentru o serie de variabile aleatoare care converge cu probabilitatea 1. Faptul acestei convergențe este o consecință ușoară fie a teoremei celor trei serii Kolmogorov, fie a inegalității maxime Kolmogorov, strâns legată de aceasta. Byron Schmuland de la Universitatea din Alberta a examinat în continuare proprietățile seriei armonice aleatoare și a arătat că seria convergentă este o variabilă aleatoare cu unele proprietăți interesante. ⁻⁴² Lucrarea lui Schmuland explică de ce această probabilitate este atât de apropiată de, dar nu exact, 1/8. Valoarea exactă a acestei probabilități este dată de integrala infinită a produsului cosinusului $C 2$ împărțită la $π.$

Seriile armonice epuizate

Se poate demonstra că seria armonică sărăcită în care sunt eliminați toți termenii în care cifra 9 apare oriunde în numitor converge, iar valoarea sa este mai mică de 80. De fapt, atunci când toți termenii care conțin un anumit șir de cifre (în orice bază) sunt eliminați, seria converge.

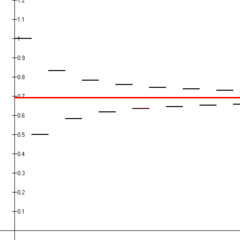
Primele paisprezece sume parțiale ale seriei armonice alternante (segmente de linie neagră), reprezentate convergente către logaritmul natural al lui 2 (linie roșie).

Aplicații

Seria armonică poate fi contraintuitivă. Acest lucru se datorează faptului că este o serie divergentă, chiar dacă termenii seriei devin mai mici și se apropie de zero. Divergența seriei armonice este sursa unor paradoxuri.

"Viermele de pe banda de cauciuc". Să presupunem că un vierme se târăște de-a lungul unei benzi de cauciuc de un metru, infinit elastice, în același timp în care banda de cauciuc este întinsă uniform. Dacă viermele se deplasează cu 1 centimetru pe minut, iar banda se întinde cu 1 metru pe minut, va ajunge viermele vreodată la capătul benzii de cauciuc? Răspunsul, în mod contraintuitiv, este "da", deoarece, după $n$ minute, raportul dintre distanța parcursă de vierme și lungimea totală a elasticului este

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.}. ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Deoarece seria devine arbitrar de mare pe măsură ce $n$ devine mai mare, în cele din urmă acest raport trebuie să depășească 1, ceea ce implică faptul că viermele ajunge la capătul elasticului. Cu toate acestea, valoarea lui $n$ la care se produce acest lucru trebuie să fie extrem de mare: aproximativ e $100$ , un număr care depășește 10⁴³ minute (10³⁷ ani). Deși seria armonică diverge, aceasta o face foarte încet.

Problema Jeep se referă la cât de mult combustibil total este necesar pentru ca o mașină cu o capacitate limitată de transport de combustibil să traverseze un deșert, lăsând picături de combustibil de-a lungul traseului. Distanța pe care mașina o poate parcurge cu o anumită cantitate de combustibil este legată de sumele parțiale ale seriilor armonice, care cresc logaritmic. Și astfel, combustibilul necesar crește exponențial cu distanța dorită.

Problema stivuirii de blocuri: dată fiind o colecție de piese de domino identice, este posibil să le stivuiți pe marginea unei mese astfel încât să atârne peste marginea mesei fără să cadă. Rezultatul contraintuitiv este că acestea pot fi stivuite într-un mod care face ca depășirea să fie oricât de mare se dorește. Asta, cu condiția să existe suficiente piese de domino.

Un înotător care merge mai repede de fiecare dată când atinge peretele piscinei. Înotătorul începe să traverseze un bazin de 10 metri cu o viteză de 2 m/s, iar la fiecare traversare se adaugă încă 2 m/s la viteza sa. În teorie, viteza înotătorului este nelimitată, dar numărul de traversări ale bazinului necesar pentru a ajunge la această viteză devine foarte mare; de exemplu, pentru a ajunge la viteza luminii (ignorând relativitatea specială), înotătorul trebuie să traverseze bazinul de 150 de milioane de ori. Contrar acestui număr mare, timpul necesar pentru a atinge o anumită viteză depinde de suma seriilor la un număr dat de traversări ale bazinului:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}}\sum _{k=1}^{n}{\frac {1}{k}}.}. ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Calcularea sumei arată că timpul necesar pentru a ajunge la viteza luminii este de numai 97 de secunde.

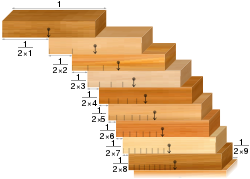
Problema stivuirii de blocuri: blocurile aliniate conform seriei armonice pun poduri de clivaje de orice lățime.

Pagini conexe

Progresia armonică
Lista sumelor de reciproce

Întrebări și răspunsuri

Î: Ce este seria armonică?

R: Seria armonică este o serie divergentă infinită în care fiecare termen este egal cu 1 împărțit la poziția sa în secvență.

Î: Ce înseamnă pentru o serie să fie divergentă?

R: Divergentă înseamnă că, pe măsură ce adăugați mai mulți termeni, suma nu încetează să crească și nu se îndreaptă spre o singură valoare finită.

Î: Ce înseamnă că o serie este infinită?

R: Infinit înseamnă că se poate adăuga întotdeauna un alt termen și că nu există un termen final al seriei.

Î: De unde provine numele acestei serii?

R: Numele acestei serii provine de la ideea de armonice în muzică, unde lungimile de undă ale supratonelor sunt 1/2, 1/3, 1/4 etc. din lungimea de undă fundamentală a coardei.

Î: Ce înseamnă o armonică?

R: O medie armonică este atunci când fiecare termen dintr-o secvență este egal cu media armonică a termenilor săi vecini. Această expresie provine, de asemenea, din muzică.

Î: Cum calculăm fiecare termen din această secvență?

R: Fiecare termen din această secvență poate fi calculat prin împărțirea lui unu la poziția sa în secvență (1/n).