Linia mondială | traiectoria unică pe care un obiect o are în timp ce călătorește atât în spațiu cât și în timp
O linie a lumii este traiectoria unică pe care un obiect o are în timp ce călătorește atât în spațiu, cât și în timp, de obicei numit spațiu-timp. Așa cum am învățat din relativitatea specială, cu cât un obiect merge mai repede, cu atât timpul încetinește mai mult pentru acel obiect. După cum puteți vedea în ilustrația din dreapta, obiectul mai lent are o trecere mai rapidă a timpului decât obiectul foarte rapid, cel pentru care timpul trece mult mai încet. Atunci când un obiect atinge viteza luminii, acesta va fi zero pe axa t, ceea ce înseamnă că nu va fi progresat deloc în direcția timpului. Practic, liniile lumii arată că, atunci când este atinsă viteza luminii, timpul se oprește pentru observator. Liniile lumii sunt foarte des utilizate în fizica teoretică și în relativitatea specială, precum și în relativitatea generală.
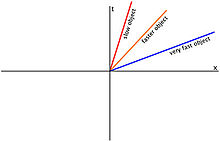
Traiectoriile distincte a trei obiecte care se deplasează cu viteze diferite și măsurătorile respective ale trecerii timpului, unde axa t reprezintă trecerea timpului, iar axa x reprezintă viteza obiectului.
Utilizare
Conceptul de linii ale lumii este utilizat pe scară largă în fizica teoretică, deoarece arată unele fapte interesante despre mișcarea de mare viteză. De exemplu, ecuația de dilatare a timpului prezentată de Albert Einstein este nedefinită din punct de vedere algebric atunci când viteza unui obiect este viteza luminii, dar, folosind liniile lumii, se poate constata că atunci când viteza este egală cu viteza luminii, timpul se va opri. Deși ecuația lui Einstein (pentru dilatarea timpului) arată că un obiect care merge mai repede decât lumina se întoarce în timp, același concept poate fi descris cu ajutorul liniilor lumii.
| Parte a unei serii de articole despre | ||||||
| Relativitatea generală | ||||||
|
| ||||||
| ·
·
| ||||||
| Concepte fundamentale
| ||||||
| Fenomene
| ||||||
| ||||||
| Soluții
| ||||||
Întrebări și răspunsuri
Î: Ce este o linie mondială?
R: O linie a lumii este traiectoria unică pe care o are un obiect în timp ce călătorește atât în spațiu, cât și în timp, de obicei numit spațiu-timp.
Î: Cum explică relativitatea specială modul în care trece timpul pentru obiectele care se deplasează cu viteze diferite?
R: Conform relativității restrânse, cu cât un obiect merge mai repede, cu atât timpul încetinește mai mult pentru acel obiect. Obiectul mai lent are o trecere mai rapidă a timpului decât obiectul foarte rapid, ceea ce înseamnă că timpul trece mult mai încet pentru acestea.
Î: Ce se întâmplă atunci când un obiect atinge viteza luminii?
R: Atunci când un obiect atinge viteza luminii, acesta va fi zero pe axa t, ceea ce înseamnă că nu va fi făcut niciun progres în direcția timpului. Acest lucru înseamnă că timpul se oprește pentru observator.
Î: În ce domenii sunt utilizate liniile lumii?
R: Liniile lumii sunt foarte des utilizate în fizica teoretică și în relativitatea specială, precum și în relativitatea generală.
Î: Cum putem vizualiza o linie a lumii?
R: Putem vizualiza o linie a lumii observând ilustrații care arată cum obiectele care se deplasează cu viteze diferite înregistrează viteze diferite de trecere a timpului.
Î: Există vreo modalitate de a schimba sau de a modifica o linie a lumii odată ce aceasta a fost stabilită?
R: Odată stabilită, o linie a lumii nu poate fi schimbată sau modificată, deoarece reprezintă o traiectorie imuabilă prin spațiu-timp.
Î: La ce se referă "axa t" în ceea ce privește atingerea vitezei luminii? R: "Axa t" se referă la progresul în termeni de timp - atunci când un obiect atinge viteza luminii, progresul său în termeni de timp este zero pe această axă, ceea ce înseamnă că nu s-a făcut niciun progres în ceea ce privește trecerea prin spațiu-timp.
Căuta în

