Scară logaritmică
O scală logaritmică este o scală utilizată atunci când există un interval mare de mărimi. Printre utilizările obișnuite se numără puterea cutremurelor, intensitatea sunetului, intensitatea luminii și pH-ul soluțiilor.
Aceasta se bazează pe ordine de mărime, mai degrabă decât pe o scară liniară standard. Valoarea fiecărui semn de pe scală este valoarea de la semnul anterior înmulțită cu o constantă.
Scalele logaritmice sunt, de asemenea, utilizate în regulile de calcul pentru înmulțirea sau împărțirea numerelor prin adăugarea sau scăderea lungimilor de pe scări.
Scara logaritmică poate fi utilă atunci când datele acoperă un interval mare de valori - logaritmul reduce acest interval la unul mai ușor de gestionat.
Unele dintre simțurile noastre funcționează în mod logaritmic (înmulțirea intensității reale a semnalului de intrare adaugă o constantă la intensitatea semnalului perceput, vezi: Legea puterii lui Stevens). Acest lucru face ca scalele logaritmice pentru aceste cantități de intrare să fie deosebit de adecvate. În special, simțul nostru auditiv percepe multiplii egali de frecvențe ca diferențe egale de înălțime.
Pe majoritatea scărilor logaritmice, multiplii mici (sau rapoarte) ai cantității de bază corespund unor valori mici (eventual negative) ale măsurii logaritmice.
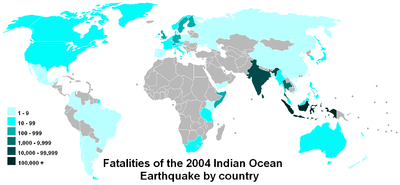
O scală logaritmică facilitează compararea valorilor care acoperă un interval mare, cum ar fi în această hartă
Cele două scări logaritmice ale unei reguli de calcul
Exemple
Exemple bine cunoscute de astfel de scale sunt:
- Scara de magnitudine Richter și scara de magnitudine a momentului (MMS) pentru puterea cutremurelor și a mișcărilor pământului.
- bel și decibel și neper pentru puterea acustică (intensitatea sonoră) și puterea electrică;
- numărarea f-stop-urilor pentru ratele de expunere fotografică;
- clasificarea probabilităților scăzute în funcție de numărul de "nouă" din expansiunea zecimală a probabilității ca acestea să nu se întâmple: de exemplu, un sistem care va eșua cu o probabilitate de 10−5este 99,999% fiabil: "cinci nouari".
- Entropia în termodinamică.
- Informația în teoria informației.
- Curbe de distribuție a dimensiunilor particulelor de sol
Unele scări logaritmice au fost concepute astfel încât valorile mari (sau raporturile) ale mărimii de bază să corespundă unor valori mici ale măsurii logaritmice. Exemple de astfel de scări sunt:
- pH pentru aciditate;
- scara de magnitudine stelară pentru luminozitatea stelelor;
O scală logaritmică este, de asemenea, o scală grafică pe una sau pe ambele fețe ale unui grafic, în care un număr x este imprimat la o distanță c-log(x) față de punctul marcat cu numărul 1. O riglă de calcul are scări logaritmice, iar nomogramele utilizează adesea scări logaritmice. Pe o scală logaritmică, o diferență egală în ordine de mărime este reprezentată de o distanță egală. Media geometrică a două numere se află la jumătatea distanței dintre ele.
Hârtia grafică logaritmică, înainte de apariția graficii computerizate, a fost un instrument științific de bază. Graficele pe hârtie cu o scală logaritmică pot evidenția legile exponențiale, iar pe hârtia log-log legile de putere, sub formă de linii drepte (a se vedea grafic semilog, grafic log-log).
Întrebări și răspunsuri
Î: Ce este o scală logaritmică?
R: O scală logaritmică este o scală utilizată atunci când există un interval mare de cantități.
Î: Care sunt câteva exemple de lucruri care pot fi măsurate pe o scară logaritmică?
R: Puterea cutremurelor, intensitatea sunetului, intensitatea luminii, rata de răspândire a epidemiilor și pH-ul soluțiilor pot fi măsurate pe o scară logaritmică.
Î: Prin ce se deosebește o scală logaritmică de o scală liniară standard?
R: O scală logaritmică se bazează pe ordine de mărime, mai degrabă decât o scală liniară standard. Valoarea fiecărui semn de pe scală este valoarea de la semnul anterior înmulțită cu o constantă.
Î: Care este avantajul utilizării unei scări logaritmice?
R: Scara logaritmică poate reduce o gamă mare de valori la o gamă mai ușor de gestionat, ceea ce poate fi util atunci când aveți de-a face cu date care acoperă o gamă largă de valori.
Î: Ce este legea de putere a lui Stevens și ce legătură are aceasta cu scările logaritmice?
R: Legea de putere a lui Stevens descrie modul în care unele dintre simțurile noastre funcționează în mod logaritmic, în care înmulțirea intensității de intrare reale adaugă o constantă la intensitatea semnalului perceput. Acest lucru face ca scalele logaritmice pentru aceste cantități de intrare să fie deosebit de adecvate.
Î: De ce este o scală logaritmică deosebit de utilă pentru măsurarea intensității sunetului?
R: Simțul nostru auditiv percepe multiplii egali de frecvențe ca diferențe egale de înălțime, astfel încât o scală logaritmică poate reprezenta cu precizie această relație dintre frecvența sunetului și intensitatea percepută.
Î: Care este relația dintre multiplii mici ai cantității de bază și măsura logaritmică de pe majoritatea scărilor logaritmice?
R: Pe majoritatea scărilor logaritmice, multiplii mici (sau rapoarte) ai cantității de bază corespund unor valori mici (eventual negative) ale măsurii logaritmice.
Căuta în