Principiul incertitudinii | numit și principiul incertitudinii Heisenberg

Diagrame

 
5. Suspendarea spațiului central cu ajutorul unui arc permite măsurarea impulsului, dar acest lucru deplasează spațiul în mod imprevizibil, astfel încât informațiile privind poziția fiecărui foton în mijloc se pierd.  


6. Această animație prezintă una dintre consecințele importante ale naturii incerte a universului: tunelarea cuantică a electronilor. Priviți cu atenție. De fiecare dată, o mică parte trece de barieră.  


4. Montarea unui arc pe o barieră cu o gaură mică face ca particula să se strecoare prin gaură, ceea ce împinge bariera, întinde arcurile și astfel măsoară impulsul. Dar, deoarece bariera montată pe arcuri se mișcă, suntem mai puțin siguri de locul în care se afla particula atunci când a trecut prin gaură, iar difracția va afecta, de asemenea, poziția acesteia pe ecranul de detecție.  


1. Fotonii, electronii și alte particule subatomice se vor focaliza cu precizie atunci când sunt proiectate printr-o gaură mare, dar nu știm cu exactitate unde se aflau în mijlocul traiectoriei lor.  


3. Îngustarea găurii crește certitudinea locului în care se află fotonul în mijloc, dar direcția sa de acolo până la ecranul de detecție din dreapta devine în mod corespunzător mai nesigură. Focalizarea devine neclară. Lărgirea găurii face ca toți fotonii să ajungă în centrul ecranului de detecție, dar atunci avem o idee mai vagă despre locul în care se aflau atunci când au trecut prin bariera centrală.  


2. Îngustarea găurii curbează traiectoriile particulelor în jurul marginilor găurii (difracție), astfel încât fasciculul rezultat devine mai mare și mai moale.  

Cum au învățat oamenii despre incertitudine?

La foarte scurt timp după ce Werner Heisenberg a creat noua fizică cuantică, ceva neașteptat a ieșit chiar din matematica sa, expresia:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad \qquad }

Intervalul de eroare în poziție (x) înmulțit cu intervalul de eroare în impuls (p) este aproximativ egal sau mai mare decât constanta Planck împărțită la 4π.

Aceste simboluri pun în formă matematică ceea ce ați văzut deja în imaginile de mai sus. Simbolurile spun, într-un mod clar, că nu poți fi perfect sigur de locul în care se află ceva și de direcția în care se îndreaptă. Dacă vă este mai clar unde se află în orice moment, atunci aveți o idee mai puțin clară despre unde se îndreaptă și cu ce viteză. Dacă vă lămuriți mai bine unde se îndreaptă și cât de repede se îndreaptă în orice moment, atunci aveți o idee mai puțin clară despre unde se află în acest moment.

Oamenii de știință aflaseră deja de ce anumite substanțe emit culori caracteristice de lumină atunci când sunt încălzite sau excitate în alt mod. Heisenberg încerca să explice de ce aceste culori au fiecare o luminozitate caracteristică. Nu ar fi fost suficient dacă el și ceilalți oameni de știință ar fi spus doar "Ei bine, așa stau lucrurile". Ei erau siguri că trebuie să existe un motiv întemeiat pentru aceste diferențe și pentru faptul că rapoartele dintre intensitățile liniilor luminoase erau întotdeauna aceleași pentru fiecare eșantion al unui element.

Habar nu avea că va da peste un secret ascuns al naturii atunci când a pornit să descopere explicația intensității liniilor colorate caracteristice fiecărui element. Studiul mecanicii cuantice demonstrase deja de ce hidrogenul are patru linii luminoase în partea spectrului pe care oamenii o pot vedea. Trebuie să fi părut că următorul lucru de învățat ar fi fost pur și simplu cum să se calculeze luminozitatea acestora. Hidrogenul părea a fi locul evident de unde să înceapă, deoarece hidrogenul are un singur electron de care trebuie să se ocupe și doar patru linii în partea vizibilă a spectrului. Cu siguranță trebuie să existe un motiv întemeiat pentru care nu sunt la fel de strălucitoare. Explicația pentru luminozitatea liniilor de culori diferite ale neonului și ale celorlalte elemente putea aștepta.

Heisenberg a început să lucreze la fizica cuantică prin adaptarea ecuațiilor clasice pentru electricitate, care sunt foarte complicate pentru început, astfel încât matematica din spatele lucrării sale din 1925 a fost foarte greu de urmărit.

El încerca să găsească modalitatea corectă de a calcula intensitatea liniilor luminoase din spectrul lămpii cu hidrogen. Trebuia să găsească o mărime conexă numită "amplitudine" și să înmulțească amplitudinea cu amplitudinea (sau, cu alte cuvinte, trebuia să ridice amplitudinea la pătrat) pentru a obține intensitatea dorită. A trebuit să găsească o modalitate de a exprima amplitudinea într-un mod care să țină cont de faptul că lămpile cu hidrogen nu radiază la toate frecvențele și nu radiază într-o gamă continuă de frecvențe în partea spectrului pe care oamenii o pot vedea. Heisenberg a găsit un nou mod remarcabil de a calcula amplitudinea.

Ecuația ciudată pe care Heisenberg a descoperit-o și a folosit-o pentru a înmulți o mărime cuantică (de exemplu, poziția) cu o alta (de exemplu, impulsul) a fost publicată în ceea ce a fost numit "lucrarea "magică" a lui Heisenberg din iulie 1925".

C ( n , n - b ) = ∑ a A A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Matematica de mai sus pare foarte grea, dar matematica care duce la ea este mult mai grea și este extrem de greu de înțeles. Ea este prezentată aici doar pentru a arăta cum arată. Lucrarea lui Heisenberg este un punct de reper istoric. Mulți dintre fizicienii care i-au citit lucrarea au spus că nu au putut să nu fie de acord cu concluziile sale, dar că nu au putut urmări explicația sa privind modul în care a ajuns la aceste concluzii. Ecuațiile de început pe care Heisenberg le-a folosit implicau serii Fourier și implicau mulți factori. Vom reveni la ecuația de mai sus, deoarece este un fel de rețetă pentru scrierea și multiplicarea matricelor.

Noile ecuații trebuiau să fie atât de ciudate și neobișnuite deoarece Heisenberg descria o lume ciudată în care unele lucruri, cum ar fi orbitele electronilor, nu se măresc sau se micșorează încet. Noile tipuri de schimbări implică salturi și intervale mari între salturi. Electronii pot sări doar între anumite orbite, iar energia câștigată sau pierdută în schimbarea între orbite este produsă atunci când este absorbit un foton cu energia potrivită sau când este produs un nou foton cu energia potrivită. Dacă electronii din atomii de hidrogen sar cel mai frecvent în jos (cad) între două anumite orbite, atunci vor fi emiși mai mulți fotoni la acel nivel de energie și, prin urmare, lumina produsă la acel nivel va fi cea mai intensă.

A fost dificil să se adapteze ecuațiile construite pentru spectre continue (ceea ce vedeți atunci când treceți lumina soarelui printr-o prismă) la spectre care au doar câteva frecvențe de vârf între care nu există nimic. Aproape tot ceea ce se învățase deja despre lumină și energie fusese realizat cu obiecte mari, cum ar fi lumânări aprinse sau sori, iar aceste obiecte mari produc toate spectre continue. Chiar dacă aceste obiecte de dimensiuni obișnuite erau ușor de experimentat, a fost nevoie de mult timp pentru a descoperi legile (fizicii) care le guvernează. Acum, fizicienii aveau de-a face cu lucruri prea mici pentru a le vedea, lucruri care nu produceau spectre continue, și încercau să găsească o modalitate de a obține măcar indicii din ceea ce știau deja, care să-i ajute să găsească legile acestor surse de lumină mici și lacunare.

Ecuațiile inițiale se refereau la un fel de corp vibrant care ar produce o undă, la fel ca o ancie într-o orgă care ar produce o undă sonoră cu o frecvență caracteristică. Așadar, exista o mișcare înainte și înapoi (ca și vibrația unei trestii) și exista o undă emisă care putea fi reprezentată grafic sub forma unei unde sinusoidale. O mare parte din ceea ce fusese descoperit anterior despre fizica la nivel atomic avea legătură cu electronii care se mișcă în jurul nucleelor. Atunci când o masă se mișcă pe o orbită, când se rotește în jurul unui fel de nucleu, aceasta are ceea ce se numește "moment unghiular". Momentul unghiular este modul în care ceva precum un carusel va continua să se rotească după ce oamenii au încetat să îl mai împingă. Matematica folosită pentru calculele de fază și momentul unghiular este complicată. În plus, Heisenberg nu a arătat toate calculele sale în lucrarea sa din 1925, astfel încât chiar și matematicienii buni ar putea avea probleme în completarea a ceea ce nu a spus.

Chiar dacă mulți fizicieni au declarat că nu au putut înțelege diferitele etape matematice din lucrarea revoluționară a lui Heisenberg, un articol recent care încearcă să explice cum a ajuns Heisenberg la rezultatul său folosește douăzeci de pagini pline de matematică. Chiar și acel articol nu este ușor de înțeles. Matematica a început cu niște chestii foarte dificile și, în cele din urmă, avea să producă ceva relativ simplu, care este prezentat în partea de sus a acestui articol. Obținerea rezultatului mai simplu nu a fost ușoară, iar noi nu vom încerca să arătăm procesul de trecere de la o imagine învechită a universului la noua fizică cuantică. Avem nevoie doar de suficiente detalii pentru a arăta că, aproape imediat ce Heisenberg a făcut descoperirea sa, a apărut o parte a modului în care funcționează universul pe care nimeni nu o mai văzuse până atunci.

Heisenberg trebuie să fi fost foarte entuziasmat, dar și foarte obosit când, noaptea târziu, a făcut în sfârșit descoperirea și a început să își demonstreze că va funcționa. Aproape imediat a observat ceva ciudat, ceva ce a crezut că este o mică problemă enervantă pe care ar putea să o facă să dispară cumva. Dar s-a dovedit că această mică neplăcere era o mare descoperire.

Heisenberg lucrase la multiplicarea amplitudinilor prin amplitudini, iar acum Heisenberg avea o modalitate bună de a exprima amplitudinea folosind noua sa ecuație. În mod firesc, el se gândea la înmulțire și la modul în care ar fi multiplicat lucruri care erau date în termenii unor ecuații complicate.

Heisenberg și-a dat seama că, pe lângă ridicarea la pătrat a amplitudinii, va dori în cele din urmă să înmulțească poziția cu impulsul sau să înmulțească energia cu timpul, și se pare că ar fi o diferență dacă ar inversa ordinea în aceste cazuri noi. Heisenberg nu credea că ar trebui să conteze dacă se înmulțește poziția cu impulsul sau dacă se înmulțește impulsul cu poziția. Dacă ar fi fost vorba doar de numere simple, nu ar fi existat nicio problemă. Dar ambele erau ecuații complicate, iar modul în care obțineai numerele pentru a le introduce în ecuații se dovedea a fi diferit în funcție de modul în care începeai. În natură trebuia să măsori poziția și apoi să măsori impulsul, sau trebuia să măsori impulsul și apoi să măsori poziția, iar în matematică a prevalat aceeași situație generală. (Vedeți articolul din Wikipedia în limba engleză Heisenberg's entryway to matrix mechanics, dacă doriți să aflați detaliile complicate!) Diferențele minuscule, dar enervante, dintre rezultate urmau să rămână, oricât de mult și-ar fi dorit Heisenberg ca ele să dispară.

În acel moment, Heisenberg nu a putut scăpa de acea mică problemă, dar era epuizat, așa că și-a predat munca supervizorului său imediat, Max Born, și a plecat în vacanță.

Max Born a fost un matematician remarcabil, care a văzut curând că ecuația pe care i-o dăduse Heisenberg era un fel de rețetă pentru scrierea unei matrice. Dr. Born a fost unul dintre puținii oameni din acea vreme care era interesat de acest tip ciudat de matematică despre care majoritatea oamenilor credeau că nu era bun la mare lucru. El știa că matricile pot fi înmulțite, astfel încât efectuarea tuturor calculelor pentru contabilizarea unei probleme de fizică putea fi rezolvată prin înmulțirea unei matrice cu alta. Simplul fapt de a putea pune o procedură complicată într-o formă standard și acceptabilă ar face-o mai ușor de lucrat. De asemenea, ar putea fi mai ușor de acceptat de către alte persoane.

Born era un matematician atât de bun încât și-a dat seama aproape imediat că schimbarea ordinii de înmulțire a celor două matrici ar produce un rezultat diferit, iar rezultatele ar fi diferit cu o cantitate mică. Această cantitate ar fi h/2πi. În viața de zi cu zi, această diferență ar fi atât de mică încât nici măcar nu am putea să o vedem.

 
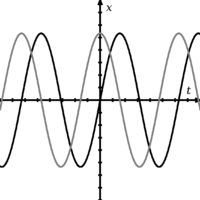
Două unde care sunt defazate una față de cealaltă  


Spectrul hidrogenului  


Spectrul de neon  


Spectrul vizual complet al soarelui. Nu există lacune. Această diagramă arată intensitățile la diferite frecvențe.  


Atunci când anumite molecule sunt excitate, ele emit o culoare caracteristică.  

Spre o teorie formală a incertitudinii

A durat câțiva ani, dar Heisenberg a reușit să demonstreze Principiul Incertitudinii, care spune că Δx × Δp = h/2, care este numărul care rezultă din ecuațiile originale, dar nu include π și i, care au legătură cu schimbările de fază. Heisenberg a explicat că și-a derivat principiul incertitudinii din acest rezultat anterior, atunci când a scris o lucrare în 1927 în care a prezentat această teorie.

Constanta scrisă h, numită constanta Planck, este un număr misterios care apare adesea, așa că trebuie să înțelegem ce este acest număr mic. Din punct de vedere numeric, este de obicei dat ca fiind 6,62607×10^-34 J s (secunde joule). Așadar, este o cantitate care implică energie și timp.

A fost descoperită atunci când Planck și-a dat seama că energia unui radiator perfect (numit radiator de corp negru) este emisă în unități de mărime definită numite "cuante" (singularul acestui cuvânt este "quantum"). Energia radiată este emisă sub formă de fotoni, iar frecvența unui foton este proporțională cu "pumnul" pe care îl dă. Diferitele frecvențe ale luminii vizibile sunt percepute de noi ca fiind culori diferite. La capătul violet al spectrului, fiecare foton are o cantitate relativ mare de energie; la capătul roșu al spectrului, fiecare foton are o cantitate relativ mică de energie. Modul de calcul al cantității de energie a unui foton este dat de ecuația E = hν (energia este egală cu constanta Planck înmulțită cu "nu" sau frecvența).

Principiul de incertitudine Heisenberg Δx × Δp ≥ h ne spune că, ori de câte ori încercăm să stabilim anumite perechi de numere, nu ne putem apropia decât într-o anumită măsură și că, dacă încercăm să ne clarificăm cu privire la unul dintre ele, adică dacă încercăm să micșorăm Δx pentru a avea o idee mai clară despre poziția unui lucru, atunci va trebui să obținem un număr mai mare pentru celălalt număr din pereche, iar diferența dintre cele două numere este strâns legată de h.

O altă pereche de mărimi fizice este conformă cu relația de incertitudine: ΔE × Δt ≥ h, iar această pereche indică, printre altele, că dacă ne uităm în spațiul interstelar, într-un loc unde nu ne așteptăm să găsim nimic, și reducem Δt din ce în ce mai aproape de 0, atunci, pentru a păstra echilibrul indicat în ecuație, ΔE trebuie să devină din ce în ce mai mare - și brusc, ceva cu impuls poate să apară în existență doar pentru acea scurtă perioadă de timp.

Cum se explică această nedeterminare (lipsa de certitudine)? Ce se întâmplă în Univers? Se spune adesea că o nouă teorie care are succes poate furniza noi informații despre fenomenele investigate. Heisenberg a creat un model matematic care a prezis intensitățile corecte pentru spectrul de linii luminoase al hidrogenului, dar, fără să aibă intenția de a face acest lucru, a descoperit că anumite perechi de mărimi fizice dezvăluie o incertitudine neașteptată. Până în acel moment, nimeni nu avusese idee că măsurătorile nu pot fi făcute la nesfârșit din ce în ce mai precise și mai exacte. Faptul că ele nu puteau fi făcute mai sigure, mai precise, a fost o nouă descoperire uimitoare. Mulți oameni nu erau dispuși să o accepte.

Bohr și colegii săi au susținut că fotonii, electronii etc. nu au nici poziție, nici impuls până când nu sunt măsurați. Această poziție teoretică a apărut în urma descoperirii incertitudinii și nu a fost doar o preferință personală cu privire la ceea ce trebuie să credem. Bohr spunea că nu știm nimic despre ceva precum un foton sau un electron până când nu îl observăm. Pentru a observa un lucru atât de mic, trebuie să interacționăm cumva cu el. În viața de zi cu zi, este posibil să facem ceva de genul mersului pe lângă un automobil în timp ce notăm momentele în care acesta traversează puncte de pe o grilă desenată pe trotuar. Poate că însăși greutatea automobilului va apăsa niște mici pârghii în pavaj care vor opri ceasurile atașate la fiecare dintre ele și vor înregistra greutatea automobilului. În final, vom avea o evidență clară a locului în care se află automobilul în diferite momente și vom putea calcula direcția de deplasare și greutatea acestuia. Am putea astfel să cunoaștem, în orice moment al ceasului, atât poziția sa, cât și impulsul său (viteza sa înmulțită cu masa sa). Nici măcar nu ne-am putea imagina că forța necesară pentru a mișca micile pârghii ar avea vreo influență asupra progresului mașinii. De asemenea, nu ne-am imagina că automobilul nu ar avea nicio locație sau traiectorie între punctele de pe trotuar în care există pârghii, sau că mașina există într-un fel de ceață tridimensională în acele momente și că se așează doar în timp ce apasă o pârghie. Lumea cu care suntem familiarizați nu dezvăluie aceste tipuri ciudate de interacțiuni.

Pentru a localiza o navă pe mare în timpul celei mai întunecate nopți am putea folosi un reflector, iar lumina nu ar perturba poziția sau direcția de deplasare a navei, dar pentru a localiza un electron cu ajutorul luminii ar fi nevoie să îl lovim cu unul sau mai mulți fotoni, fiecare dintre ei având suficient momentum pentru a perturba poziția și traiectoria electronului. Localizarea electronului cu alte mijloace ar implica menținerea acestuia într-un fel de constrângere fizică care ar pune capăt, de asemenea, mișcării sale de înaintare.

Pentru a localiza un foton, cel mai bun lucru care se poate face fără a-i întrerupe mișcarea de înaintare este să îl facem să treacă printr-o gaură circulară într-o barieră. Dacă se cunoaște momentul în care fotonul a fost emis (de către un laser, de exemplu) și momentul în care fotonul ajunge la un ecran de detecție, cum ar fi o cameră digitală, atunci este posibil să se calculeze timpul necesar pentru a parcurge această distanță și momentul în care fotonul a trecut prin gaură. Cu toate acestea, pentru a permite fotonului să treacă prin ea, gaura circulară trebuie să aibă un diametru mai mare decât dimensiunea fotonului. Cu cât gaura circulară este mai mică, cu atât ne apropiem mai mult de cunoașterea poziției exacte a fotonului atunci când trece prin ea. Cu toate acestea, nu putem ști niciodată dacă fotonul este descentrat în acel moment. Dacă gaura are exact aceeași dimensiune ca și fotonul, acesta nu va trece prin ea. Pe măsură ce diametrul găurii este micșorat, impulsul sau direcția fotonului la ieșirea din gaură se modifică din ce în ce mai mult.

Niels Bohr și colegii săi au argumentat că avem mari probleme dacă presupunem că sunt adevărate lucrurile care sunt prea mici pentru a fi văzute chiar și cu un microscop, dar pentru care avem dovezi doar la scara vieții de zi cu zi. În viața de zi cu zi, lucrurile au o poziție definită în orice moment. La scară atomică, nu avem nicio dovadă care să susțină această concluzie. În viața de zi cu zi, lucrurile au un moment precis în care se produc. La scară atomică, nu avem nicio dovadă care să susțină această concluzie. În viața de zi cu zi, dacă cineva observă o fabrică din schimbul de noapte al primei zile până în schimbul de zi al celei de-a doua și vede un automobil terminat rulând la docurile de expediere, nu ar avea sens să spunem că este imposibil de spus dacă a fost livrat în timpul schimbului de noapte sau în timpul schimbului de zi. Dar, la scară atomică, putem arăta cazuri în care trebuie să numărăm un singur foton ca fiind produs în două momente. (Dacă acest lucru nu este suficient de rău, putem arăta și cazuri în care un singur foton este produs de două lasere adiacente).

O parte din dificultatea de a afla ce se întâmplă la scară atomică constă în faptul că am dori să știm atât unde se află ceva, cât și care este traiectoria sa și să știm ambele lucruri în același timp, dar nu putem măsura atât poziția, cât și traiectoria în același timp. Fie măsurăm impulsul unui foton sau al unui electron la un moment dat și apoi, fără mai multă întârziere decât este necesar, măsurăm poziția acestuia, fie inversăm lucrurile și măsurăm mai întâi poziția și apoi impulsul. Problema este că, făcând ca prima măsurătoare să ia o formă destul de precisă (prin apăsarea ei într-un fel sau altul), creștem incertitudinea implicată în următoarea măsurătoare. Dacă măsurătorile noastre inițiale au fost atât de rudimentare încât în fiecare dintre ele au fost introduse multe erori, atunci am putea îmbunătăți lucrurile folosind o atingere mai ușoară pentru fiecare dintre ele, dar nu am putea niciodată să depășim o anumită limită de precizie.

Știm din viața de zi cu zi că încercarea de a cântări ceva pe un cântar de baie plasat pe o mașină de spălat în ciclu de centrifugare va produce rezultate inexacte, deoarece acul cântarului se va mișca rău de tot. Putem opri mașina de spălat. Dar, pentru măsurători foarte precise, constatăm că trecerea camioanelor prin cartier face ca acul să se clatine, așa că putem pune cântarul pe un obiect care să-l izoleze de perturbațiile exterioare. Credem că putem elimina suficient de mult vibrațiile pentru a obține rezultate la fel de precise precum ne dorim. Nu luăm niciodată în considerare faptul că lucrul de pe cântar este el însuși în vibrație sau că posedă un impuls indefinit.

Pornind de la principiul incertitudinii, se pare că, de fapt, nu există nici o poziție definită și nici un moment definit pentru orice lucru la scară atomică și că experimentatorii pot doar să forțeze lucrurile să fie definite în limitele stabilite de principiul incertitudinii. Bohr și colegii săi au susținut doar că nu putem ști nimic fără a face măsurători, iar atunci când se fac măsurători putem împinge lucrurile în direcția unei poziții mai definite sau a unui moment mai definit, dar că nu putem obține o definiție sau o certitudine absolută, așa cum ne-am dori. Dar alții au luat în serios această posibilitate și au susținut că, dacă matematica este corectă, atunci nu poate exista definiție sau certitudine în lumea celor foarte mici. Natura științei constă în faptul că matematica este doar un model al realității și nu există nicio garanție că este un model corect.

Matematica și consecințele practice ale lucrurilor pe care matematica le prezice sunt atât de fiabile încât este foarte greu să nu fii de acord cu ele, dar ceea ce spune matematica despre lumea reală a produs mai multe idei diferite. Printre oamenii de știință care au lucrat cu Niels Bohr la Copenhaga, principiul incertitudinii a fost considerat ca însemnând că, la un nivel elementar, universul fizic nu există într-o formă deterministă. Mai degrabă, este o colecție de probabilități sau potențiale.

Contrar poveștii țesute în jurul matematicii de către grupul de la Copenhaga, există și alte povești, cum ar fi "interpretarea universurilor multiple", care spune că, de fiecare dată când există mai multe rezultate posibile conform teoriei cuantice, fiecare rezultat apare în propriul său univers nou. Einstein a susținut că nu există rezultate multiple posibile, deci există un singur univers și acesta este determinat sau, după cum a spus el, "Dumnezeu nu joacă zaruri".

 
Dacă h ar fi cea mai mică cantitate de energie posibilă, atunci ecuația de bază care arată energia conținută în fotoni de diferite frecvențe nu s-ar echilibra. Ar fi greșită.  

Obiecții împotriva principiului incertitudinii

Albert Einstein a văzut că noua mecanică cuantică implica lipsa poziției și a momentului în timpul anterior efectuării măsurătorilor și a obiectat vehement. El credea cu tărie că lucrurile aveau poziții definite și momente definite înainte de a fi măsurate și că faptul că măsurarea unuia dintre două lucruri și perturbarea posibilității de a măsura cu precizie celălalt lucru nu argumentează că ar exista o lipsă a oricăruia dintre ele înainte. El și doi dintre colegii săi au scris ceea ce a ajuns să fie cunoscut sub numele de "lucrarea EPR". Această lucrare susține că trebuie să existe caracteristici care să determine poziția și impulsul și că, dacă le-am putea vedea sau dacă am putea obține informații despre acestea, atunci am putea cunoaște și prezice matematic poziția și impulsul. Multă vreme, oamenii au crezut că nu există nicio modalitate de a dovedi sau infirma ceea ce pentru Einstein era un articol de credință. Argumentul a fost foarte productiv, deoarece a dus la toate dezvoltările moderne în domeniul entanglementului.

Din punct de vedere matematic, Einstein s-a dovedit a fi greșit. În 1964, John Stewart Bell a dezvoltat o metodă matematică pentru a face distincția între comportamentul a două particule care au stări determinate, care sunt pur și simplu necunoscute celor doi indivizi care le investighează, și două particule care au stări încurcate, care sunt nedeterminate sau incerte până când sunt măsurate. Metoda sa arată că probabilitățile de a obține anumite rezultate sunt diferite în cele două ipoteze diferite. Lucrarea sa se numește Teorema lui Bell sau Inegalitatea lui Bell. Experimentele au demonstrat că natura se comportă așa cum o descrie Bell.

 

O altă cale spre incertitudine

Discuțiile inițiale despre principiul de incertitudine al lui Heisenberg se bazau pe un model care nu lua în considerare faptul că particulele de materie, cum ar fi electronii, protonii etc., au o lungime de undă. În 1926, Louis de Broglie a demonstrat că toate lucrurile, nu doar fotonii, au propria lor frecvență. Lucrurile au o natură de undă și o natură de particulă, la fel ca și fotonii. Dacă încercăm să facem unda unui lucru, cum ar fi un proton, mai îngustă și mai înaltă, poziția sa va fi mai clară, dar atunci impulsul va fi mai puțin bine definit. Dacă încercăm să facem ca partea de momentum a descrierii unei unde să fie mai clară, adică să o facem să rămână într-un interval mai restrâns de valori, atunci vârful undei se împrăștie și poziția sa devine mai puțin definită.

Unda care face parte din descrierea unui foton nu este, în mecanica cuantică, același lucru cu o undă de pe suprafața oceanului sau cu regiunile de aer comprimat și aer rarefiat care formează undele sonore. În schimb, aceste unde au vârfuri sau regiuni de mare amplitudine care au legătură cu probabilitatea de a găsi ceva în acel punct din spațiu și timp. Mai exact, pătratul amplitudinii este cel care dă probabilitatea de apariție a unui anumit fenomen.

Unda care se aplică unui foton poate fi o undă sinusoidală pură. În acest caz, pătratul valorii fiecărui vârf ar da probabilitatea de a observa fotonul în acel punct. Deoarece amplitudinile undelor sinusoidale sunt pretutindeni aceleași, probabilitatea de a găsi fotonul în fiecare dintre ele ar fi aceeași. Așadar, practic, cunoașterea undei pentru unul dintre acești fotoni nu ar oferi niciun indiciu despre locul în care să îl căutăm. Pe de altă parte, impulsul unui foton este legat matematic de amplitudinea undei sale. Deoarece în acest caz avem o undă sinusoidală pură, amplitudinea fiecărui ciclu al undei este aceeași și, prin urmare, există o singură valoare a impulsului asociată cu această undă. Nu am ști unde va lovi fotonul, dar am ști exact cât de tare va lovi.

În cazul fasciculelor de lumină care se concentrează asupra unui punct de pe un ecran de detecție, undele asociate fotonilor nu sunt unde sinusoidale pure. În schimb, acestea sunt unde cu amplitudine mare într-un punct și amplitudini mult mai mici de o parte și de alta a vârfului maxim. Din punct de vedere matematic, este posibil să se analizeze o astfel de undă într-un număr de unde sinusoidale diferite cu lungimi de undă diferite. Este puțin mai ușor de vizualizat inversul acestui proces, analizând o undă sinusoidală inițială de o frecvență la care se adaugă o a doua undă sinusoidală de o lungime de undă diferită, apoi o a treia, apoi o a patra și așa mai departe. Rezultatul va fi o undă complexă care prezintă un vârf înalt și care conține un număr mare de unde cu lungimi de undă diferite și, prin urmare, cu momente diferite. În acest caz, probabilitatea ca fotonul să apară într-un anumit punct este extrem de mare, dar impulsul pe care îl furnizează se poate dovedi a fi legat de lungimea de undă a oricăreia dintre undele componente. Cu alte cuvinte, valoarea p = ħ/λ nu mai este o valoare unică, deoarece trebuie luate în considerare toate lungimile "undelor de lungimi de undă diferite" asamblate.

Simularea arată modul în care se poate modela matematic creșterea intensității localizării unei particule: Suprapuneți mai multe forme de undă diferite peste unda sinusoidală originală. Centrul va forma un vârf din ce în ce mai înalt, iar restul vârfurilor vor crește în număr, dar vor scădea în înălțime, deoarece vor interfera unele cu altele. Astfel, în final, există multe unde diferite în suprapunere, fiecare cu o lungime de undă diferită și (prin p = ħ/λ) un moment diferit, dar numai un singur vârf foarte înalt, unul care crește din ce în ce mai mult și se îngustează și ne oferă ceva din ce în ce mai aproape de o poziție determinată.

Pentru ca impulsul să fie din ce în ce mai definit, ar trebui să eliminăm din ce în ce mai mult din undele sinusoidale suprapuse, până când vom avea doar o undă sinusoidală simplă. În acest fel, am diminua progresiv înălțimea vârfului central și am crește progresiv înălțimile locurilor concurente în care s-ar putea găsi particula.

Așadar, atunci când începem cu o imagine ondulatorie a particulelor subatomice, în mod normal, vom avea întotdeauna de-a face cu cazuri cu vârfuri centrale relativ înalte și cu lungimi de undă relativ numeroase. În aceste condiții, nu se va putea prezice niciodată o poziție exactă sau un moment exact. Dacă modelul matematic este o reprezentare exactă a lumii reale, atunci nici un foton sau altă particulă subatomică nu are o poziție exactă sau un moment precis. Atunci când măsurăm o astfel de particulă, putem alege o metodă care comprimă și mai mult vârful și îl face mai îngust, sau putem alege o metodă care scade vârful și uniformizează lungimile de undă componente. În funcție de ceea ce măsurăm și de modul în care o măsurăm, putem face ca locația noastră să iasă mai precisă sau putem face ca intervalul de momentum să fie mai îngust. Putem avea grijă, în proiectarea experimentului, să evităm diversele moduri de a manipula aparatul, dar nu putem scăpa de faptul că, pentru început, nu a existat nimic complet definit.

 
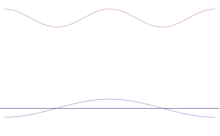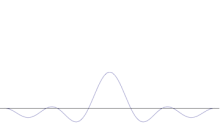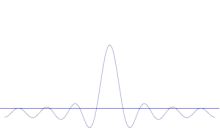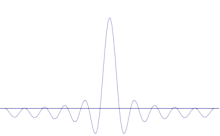
Suprapunerea mai multor unde plane. Pachetul de unde devine din ce în ce mai localizat odată cu adăugarea mai multor unde. Transformarea Fourier este o operație matematică care separă un pachet de unde în unde plane individuale. Rețineți că undele prezentate aici sunt reale doar în scop ilustrativ, în timp ce în mecanica cuantică funcția de undă este, în general, complexă.  

Influențe culturale

Principiul de incertitudine Heisenberg a influențat foarte mult argumentele privind liberul arbitru. Conform teoriilor fizicii clasice, este posibil să se susțină că legile cauzei și efectului sunt inexorabile și că, odată ce universul a început într-un anumit mod, interacțiunile dintre toată materia și energia care vor apărea în viitor pot fi calculate pornind de la acea stare inițială. Deoarece totul este în mod absolut rezultatul a ceea ce a precedat, susțineau ei, fiecare decizie pe care o ia o ființă umană și fiecare situație în care aceasta intră a fost predeterminată încă de la începutul timpului. Prin urmare, nu avem nicio alegere în ceea ce facem.

Cei care cred în liberul arbitru susțin că legile mecanicii cuantice nu prezic ce se va întâmpla, ci doar ce este mai mult și ce este mai puțin probabil să se întâmple. Prin urmare, fiecare acțiune este rezultatul unei serii de "aruncări aleatorii cu banul" și nicio decizie nu ar putea fi urmărită până la un set de condiții prealabile necesare.

Expresiile "salt cuantic" și "salt cuantic" au devenit moduri obișnuite de a vorbi despre lucruri. De obicei, oamenii intenționează să descrie ceva ca implicând o schimbare uriașă care are loc într-o perioadă scurtă de timp. De fapt, termenul se aplică la modul în care se comportă un electron într-un atom, fie atunci când acesta absoarbe un foton care vine din exterior și astfel sare de pe o orbită în jurul nucleului atomului pe o orbită superioară, fie atunci când emite un foton și astfel cade de pe o orbită superioară pe o orbită inferioară. Ideea lui Niels Bohr și a colegilor săi a fost că electronul nu se deplasează între orbite, ci dispare de pe o orbită și apare instantaneu pe o altă orbită. Așadar, un salt cuantic nu reprezintă o schimbare cutremurătoare, ci o schimbare bruscă și minusculă.

Atunci când oamenii măsoară un proces la scară subatomică și se manifestă principiul incertitudinii, se poate spune că acțiunea umană a influențat lucrul care a fost măsurat. Efectuarea unei măsurători menite să obțină o indicație precisă a locației unei particule va influența în mod inevitabil impulsul acesteia și, indiferent de ceea ce se face pentru a măsura acel impuls cât mai curând posibil după măsurarea poziției sale, nu se poate să nu se fi schimbat probabilitățile de a descoperi ce impuls va fi descoperit. Așadar, principiul incertitudinii poate explica unele tipuri de interferențe produse de investigatori care influențează rezultatele unui experiment sau ale unei observații. Cu toate acestea, nu toate efectele observatorului se datorează efectelor cuantice sau principiului incertitudinii. Restul sunt "efecte ale observatorului", dar nu efecte de incertitudine cuantică.

Efectele observatorului includ tot felul de lucruri care operează la scara umană obișnuită a evenimentelor. Dacă un antropolog încearcă să își facă o idee clară despre viața într-o societate primitivă, dar prezența sa deranjează comunitatea pe care o vizitează, atunci observațiile făcute pot fi foarte înșelătoare. Cu toate acestea, niciuna dintre interacțiunile relevante nu are loc la nivelul descris de mecanica cuantică sau de principiul incertitudinii.

Uneori, cuvântul "cuantic" va fi folosit în scopuri publicitare pentru a indica ceva nou și puternic. De exemplu, producătorul de motoare mici pe benzină, Briggs and Stratton, are o linie de motoare cu patru cilindri și putere redusă pentru mașini de tuns iarba pe benzină și unelte de grădină similare, pe care le numește "Quantum".

 

Mai multe informații

• Introducere în teoria cuantică, p. 115 și p. 158

J.P. McEvoy și Oscar Zarate