Constanta Planck | Este numită după fizicianul Max Planck

Fond

Simboluri utilizate în acest articol.
Simbol Adică E Energie h Constanta Planck k Constanta Boltzmann c viteza luminii λ lungimea de undă a radiației ν frecvența de radiație T temperatura absolută

Între 1670 și 1900, oamenii de știință au discutat despre natura luminii. Unii oameni de știință credeau că lumina este formată din mai multe milioane de particule mici. Alți oameni de știință credeau că lumina este o undă.

Lumina: unde sau particule?

În 1678, Christiaan Huygens a scris cartea Traité de la lumiere ("Tratat despre lumină"). El credea că lumina este formată din unde. El spunea că lumina nu poate fi formată din particule, deoarece lumina din două fascicule nu ricoșează una în alta. În 1672, Isaac Newton a scris cartea Opticks. El credea că lumina este formată din particule roșii, galbene și albastre pe care le-a numit corpusculi. Newton a explicat acest lucru prin "experimentul cu două prisme". Prima prismă a împărțit lumina în diferite culori. A doua prismă a unit aceste culori în lumină albă.

În secolul al XVIII-lea, teoria lui Newton a primit cea mai mare atenție. În 1803, Thomas Young a descris "experimentul dublei fante". În acest experiment, lumina care trece prin două fante înguste interferează cu ea însăși. Acest lucru provoacă un model care arată că lumina este alcătuită din unde. În restul secolului al XIX-lea, teoria ondulatorie a luminii a primit cea mai mare atenție. În anii 1860, James Clerk Maxwell a dezvoltat ecuații care descriu radiația electromagnetică sub formă de unde.

Teoria radiațiilor electromagnetice consideră lumina, undele radio, microundele și multe alte tipuri de unde ca fiind același lucru, cu excepția faptului că au lungimi de undă diferite. Lungimea de undă a luminii pe care o putem vedea cu ochii noștri este aproximativ între 400 și 600 nm. Lungimea de undă a undelor radio variază între 10 m și 1500 m, iar lungimea de undă a microundei este de aproximativ 2 cm. În vid, toate undele electromagnetice se deplasează cu viteza luminii. Frecvența undei electromagnetice este dată de:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}} .

Simbolurile sunt definite aici.

Radiatoare de caroserie negre

Toate lucrurile calde emit radiații termice, care sunt radiații electromagnetice. Pentru majoritatea lucrurilor de pe Pământ, această radiație se află în domeniul infraroșu, dar ceva foarte fierbinte (1000 °C sau mai mult) emite radiații vizibile, adică lumină. La sfârșitul anilor 1800, mai mulți oameni de știință au studiat lungimile de undă ale radiațiilor electromagnetice emise de radiatoare de corp negru la diferite temperaturi.

Legea Rayleigh-Jeans

Lordul Rayleigh a publicat pentru prima dată principiile de bază ale legii Rayleigh-Jeans în 1900. Teoria se baza pe teoria cinetică a gazelor. Sir James Jeans a publicat o teorie mai completă în 1905. Legea relaționează cantitatea și lungimea de undă a energiei electromagnetice emise de un radiator cu corp negru la diferite temperaturi. Ecuația care o descrie este:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}} .

Pentru radiațiile cu lungimi de undă mari, rezultatele prevăzute de această ecuație au corespuns bine cu rezultatele practice obținute în laborator. Cu toate acestea, pentru lungimi de undă scurte (lumina ultravioletă), diferența dintre teorie și practică era atât de mare încât a fost supranumită "catastrofa ultravioletă".

Legea lui Planck

în 1895, Wien a publicat rezultatele studiilor sale privind radiația provenită de la un corp negru. Formula sa a fost:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Această formulă a funcționat bine pentru radiațiile electromagnetice de lungime de undă scurtă, dar nu a funcționat bine cu lungimi de undă lungi.

În 1900, Max Planck a publicat rezultatele studiilor sale. El a încercat să dezvolte o expresie pentru radiația corpului negru exprimată în termeni de lungime de undă, presupunând că radiația este formată din cuante mici și apoi să vadă ce se întâmplă dacă cuantele sunt făcute infinit de mici. (Aceasta este o abordare matematică standard). Expresia a fost:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{{\frac {hc}{\lambda kT}}-1}}} .

Dacă se permite ca lungimea de undă a luminii să devină foarte mare, atunci se poate demonstra că relațiile Raleigh-Jeans și Planck sunt aproape identice.

El a calculat h și k și a constatat că

h = 6,55×10⁻²⁷ erg-sec.

k = 1.34×10⁻¹⁶ erg-deg^-1 .

Valorile sunt apropiate de valorile acceptate în zilele noastre de 6,62606×10⁻³⁴ și, respectiv, 1,38065×10⁻¹⁶ . Legea lui Planck este în concordanță cu datele experimentale, dar semnificația sa deplină a fost apreciată abia câțiva ani mai târziu.

Teoria cuantică a luminii

Se pare că electronii sunt dislocați prin efectul fotoelectric dacă lumina atinge o frecvență de prag. Sub această frecvență, niciun electron nu poate fi emis de metal. În 1905, Albert Einstein a publicat o lucrare în care explica acest efect. Einstein a propus că un fascicul de lumină nu este o undă care se propagă prin spațiu, ci mai degrabă o colecție de pachete de unde discrete (fotoni), fiecare cu energie. Einstein a spus că efectul se datorează faptului că un foton lovește un electron. Acest lucru a demonstrat natura de particulă a luminii.

Einstein a constatat, de asemenea, că radiațiile electromagnetice cu o lungime de undă mare nu au avut niciun efect. Einstein a spus că acest lucru se datorează faptului că "particulele" nu aveau suficientă energie pentru a perturba electronii.

Planck a sugerat că energia fiecărui foton era legată de frecvența fotonului prin constanta Planck. Aceasta ar putea fi scrisă matematic astfel:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}} .

Planck a primit Premiul Nobel în 1918, ca recunoaștere a serviciilor pe care le-a adus avansării fizicii prin descoperirea cuantelor de energie. În 1921, Einstein a primit Premiul Nobel pentru legătura dintre constanta Planck și efectul fotoelectric.

 
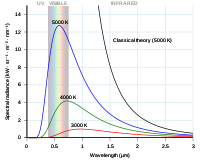
Curba Rayleigh-Jeans și curba lui Planck reprezentate în funcție de lungimea de undă a fotonului.  


Conferința Solway 1911. Planck, Einstein și Jeans sunt în picioare. Planck este al doilea din stânga. Einstein este al doilea din dreapta. Jeans este al cincilea din dreapta. Wien este așezat, al treilea din dreapta.  


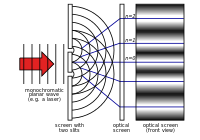
Experimentul cu două fante al lui Young  


Ilustrație preluată din scrisoarea originală a lui Newton către Royal Society (1 ianuarie 1671 [calendar iulian]). S reprezintă lumina soarelui. Lumina dintre planurile BC și DE este în culori. Aceste culori se recombină pentru a forma lumina solară pe planul GH  

Aplicație

Constanta lui Planck este importantă în multe aplicații. Câteva dintre acestea sunt enumerate mai jos.

Modelul Bohr al atomului

În 1913, Niels Bohr a publicat modelul Bohr al structurii atomului. Bohr spunea că momentul unghiular al electronilor care se deplasează în jurul nucleului poate avea doar anumite valori. Aceste valori sunt date de ecuația

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

unde

L = momentul unghiular asociat unui nivel.

n = număr întreg pozitiv.

h = constanta Planck.

Modelul Bohr al atomului poate fi utilizat pentru a calcula energia electronilor la fiecare nivel. În mod normal, electronii vor umple stările cu cel mai mic număr de puncte ale unui atom. Dacă atomul primește energie, de exemplu, de la un curent electric, electronii vor fi excitați într-o stare superioară. Electronii vor reveni apoi într-o stare inferioară și își vor pierde energia suplimentară prin emiterea unui foton. Deoarece nivelurile de energie au valori specifice, fotonii vor avea niveluri de energie specifice. Lumina emisă în acest mod poate fi împărțită în diferite culori cu ajutorul unei prisme. Fiecare element are un model propriu. Modelul neonului este prezentat alăturat.

Principiul de incertitudine al lui Heisenberg

În 1927, Werner Heisenberg a publicat principiul incertitudinii. Principiul afirmă că nu este posibil să se facă o măsurare fără a perturba lucrul măsurat. De asemenea, acest principiu stabilește o limită pentru perturbarea minimă cauzată de efectuarea unei măsurători.

În lumea macroscopică, aceste perturbații au o importanță foarte mică. De exemplu, dacă se măsoară temperatura unui balon cu lichid, termometrul va absorbi o cantitate mică de energie pe măsură ce se încălzește. Acest lucru va cauza o mică eroare în citirea finală, dar această eroare este mică și nu este importantă.

În mecanica cuantică lucrurile stau diferit. Unele măsurători se fac prin observarea modelului fotonilor împrăștiați. Un astfel de exemplu este împrăștierea Compton. În cazul în care se măsoară atât poziția, cât și momentul unei particule, principiul incertitudinii afirmă că există un compromis între precizia cu care se măsoară momentul și precizia cu care se măsoară poziția. Ecuația care descrie acest compromis este:

Δ x Δ p ⩾ h 4 π {\displaystyle \Delta x\,\Delta p\geqslant {\frac {h}{4\pi }}\qquad \qquad \qquad \qquad }

unde

Δp = incertitudinea momentului.

Δx = incertitudinea poziției.

h = constanta Planck.

Culoarea diodelor emițătoare de lumină

În circuitul electric prezentat în dreapta, căderea de tensiune pe dioda emițătoare de lumină (LED) depinde de materialul LED-ului. În cazul diodelor de siliciu, căderea este de 0,6 V. Cu toate acestea, în cazul LED-urilor, aceasta este cuprinsă între 1,8 V și 2,7 V. Aceste informații permit utilizatorului să calculeze constanta Planck.

Energia necesară pentru ca un electron să sară bariera de potențial în materialul LED este dată de

E = Q e V V L {\displaystyle E=Q_{e}V_{L}\,}

unde

Q_e este sarcina unui electron.

V_L este căderea de tensiune pe LED.

Când electronul se dezintegrează din nou, el emite un foton de lumină. Energia fotonului este dată de aceeași ecuație utilizată în cazul efectului fotoelectric. Dacă se combină aceste ecuații, lungimea de undă a luminii și tensiunea sunt legate de următoarea relație

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}}}\},}

Tabelul de mai jos poate fi calculat din această relație.

Culoare	Lungime de undă (nm)	Tensiune
lumină roșie	650	1.89
lumină verde	550	2.25
lumină albastră	470	2.62

 
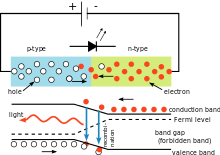
Circuit simplu cu LED-uri care ilustrează utilizarea constantei Planck. Culoarea luminii emise depinde de căderea de tensiune pe diodă. Lungimea de undă a luminii poate fi calculată cu ajutorul constantei Planck.  


Spectrul vizibil al neonului. Fiecare linie reprezintă o pereche diferită de niveluri energetice.  


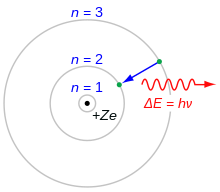
Modelul lui Bohr al atomului. Un electron care cade din învelișul n=3 în învelișul n=2 pierde energie. Această energie este transportată sub forma unui singur foton.  

Valoarea constantei Planck și redefinirea kilogramului

De la descoperirea sa, măsurătorile lui h au devenit mult mai bune. Planck a citat pentru prima dată valoarea lui h ca fiind de 6,55×10⁻²⁷ erg-sec. Această valoare este la mai puțin de 5% din valoarea actuală.

La data de 3 martie 2014, cea mai bună măsurătoare a lui h în unități SI este 6,62606957×10⁻³⁴ J-s. Cifra echivalentă în unități cgs este 6,62606957×10⁻²⁷ erg-sec. Incertitudinea relativă a lui h este de 4,4×10⁻⁸ .

Constanta Planck redusă (ħ) este o valoare care este uneori utilizată în mecanica cuantică. Aceasta se definește astfel

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}} .

Unitățile Planck sunt uneori utilizate în mecanica cuantică în loc de SI. În acest sistem, constanta Planck redusă are o valoare de 1, astfel încât valoarea constantei Planck este 2π.

Constanta Plancks poate fi acum măsurată cu o precizie foarte mare. Acest lucru a determinat BIPM să ia în considerare o nouă definiție a kilogramului. Prototipul internațional al kilogramului nu mai este utilizat pentru a defini kilogramul. În schimb, BIPM definește constanta Planck ca având o valoare exactă. Oamenii de știință folosesc această valoare și definițiile metrului și secundei pentru a defini kilogramul.

 

Valoarea constantei teoretice a lui Planck

Constanta lui Planck poate fi, de asemenea, derivată matematic:

 

h = μ 0 π 12 c 3 [ q 0 [ 0.9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{{[{q_{0}}{{[0.9163a_{0}]}^{2}]^{2}}}{f_{1r}}^{5}\cdot {s}=6.63\ ori 10^{-34}J\cdot s}

Aici, μ 0 {\displaystyle \mu _{0}} este permeabilitatea spațiului liber, c {\displaystyle c} este viteza luminii, q 0 {\displaystyle q_{0}} este sarcina electrică a electronului, a 0 {\displaystyle a_{0}} este raza lui Bohr, iar f 1 r {\displaystyle f_{1r}} este frecvența de revoluție a electronului într-un atom de hidrogen ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\ ori 10^{15}rev/s)} . Când aceste valori constante sunt substituite la constanta Planck teoretică, valoarea teoretică a constantei Planck este exact egală cu valoarea experimentală.

 Formula elementară a constantei lui Planck în funcție de raportul dintre masa protonului și cea a electronului, sarcina electronului, viteza luminii și permitivitatea vidului este derivată în. Aceasta se exprimă după cum urmează:

h = e 2 c ε 0 π 2 3 m p m e {\displaystyle h={\frac {e^{2}}{c\,\varepsilon _{0}}}}{\sqrt {\pi \,{\sqrt {\frac {2}{3}}}}\,\,{\frac {m_{p}}}{m_{e}}}}}}

unde e {\displaystyle e} este sarcina elementară a unui electron, m p {\displaystyle m_{p}} masa unui proton, m e {\displaystyle m_{e}} masa unui electron, ε 0 {\displaystyle \varepsilon _{0}} permitivitatea vidului, iar c {\displaystyle c} viteza luminii.

 

Pagini conexe

• Dualitatea undă-particulă